【典型应用2】不等式
（☆☆）【32.2.1】
求不等式|x+2|+|x-1|＞3的解集．
【解析】
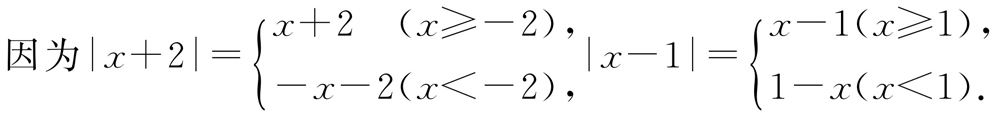
故可把全体实数x分为三个部分：①x＜-2，②-2≤x＜1，③x≥1.
所以原不等式等价于下面三个不等式组：
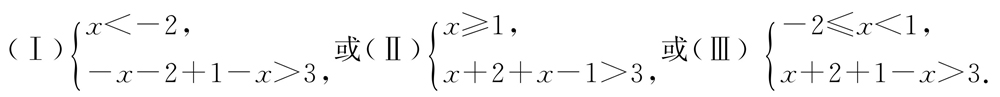
不等式组（Ⅰ）的解集是x＜-2；不等式组（Ⅱ）的解集是x＞1；不等式组（Ⅲ）的情况无解．综上可知原不等式的解集是x＜-2或x＞1.
（☆☆☆）【32.2.2】
已知关于x的不等式|x-5|+|x-3|＜a无解，求a的取值范围．
【解析】
（1）当x≤3时，原不等式可化为-x+5-x+3＜a，即a＞8-2x，由x≤3，所以-2x≥-6，故a＞2.
（2）当3＜x≤5时，原不等式可化为-x+5+x-3＜a，即a＞2.
（3）当x＞5时，原不等式可化为x-5+x-3＜a，即a＞2x-8＞10-8=2，故a＞2.
综上知a＞2时不等式有解，要使不等式无解，a≤2.
【备注】
|x-x1|+|x-x2|＜a的几何意义：数轴上到x1，x2所表示的点的距离之和小于a的点的集合．
（☆☆）【巩固练习2】
已知a，b，c≠0，且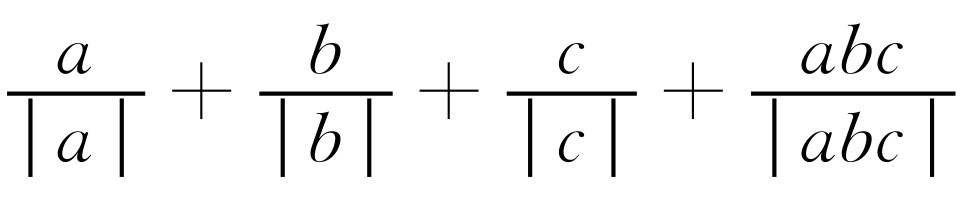
的最大值为m，最小值为n，则2015（m+n+1）=________.