初中数学代数专题1分类讨论【典型应用4】综合应用

【典型应用4】综合应用

（☆☆）【1.4.1】

某园艺公司对一块直角三角形的花圃进行改造，测得两直角边长为6m，8m．现要将其扩建成等腰三角形，且扩充部分是以原有的8m为直角边的直角三角形，求扩建后的等腰三角形花圃的周长．

【解析】

已知原来的花圃为Rt△ABC，其中BC=6m，AC=8m，∠ACB=90°．由勾股定理易知AB=10m.

①如图1-1所示，AB=AD，此时AD=10m，CD=6m．故扩建后的等腰三角形花圃的周长为12+10+10=32（m）.

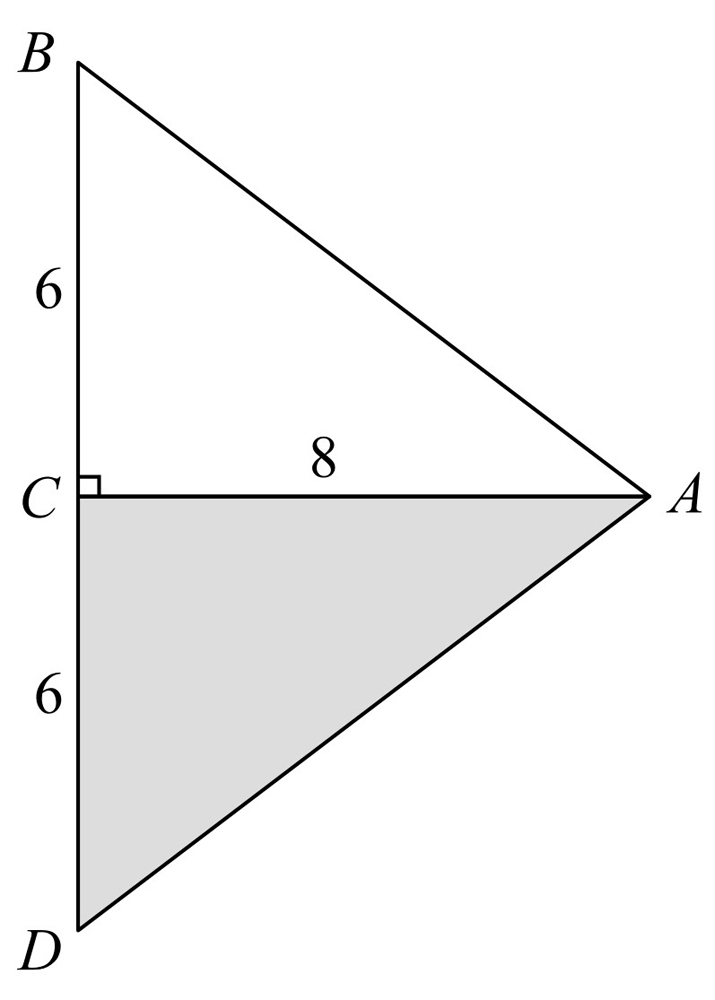
图1-1

②如图1-2所示，BD=AB=10m，在Rt△ACD中，由勾股定理得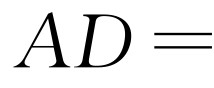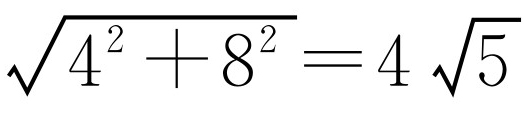，此时，扩建后的等腰三角形花圃的周长为.

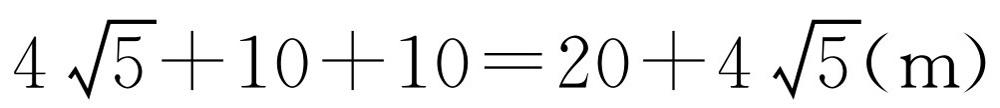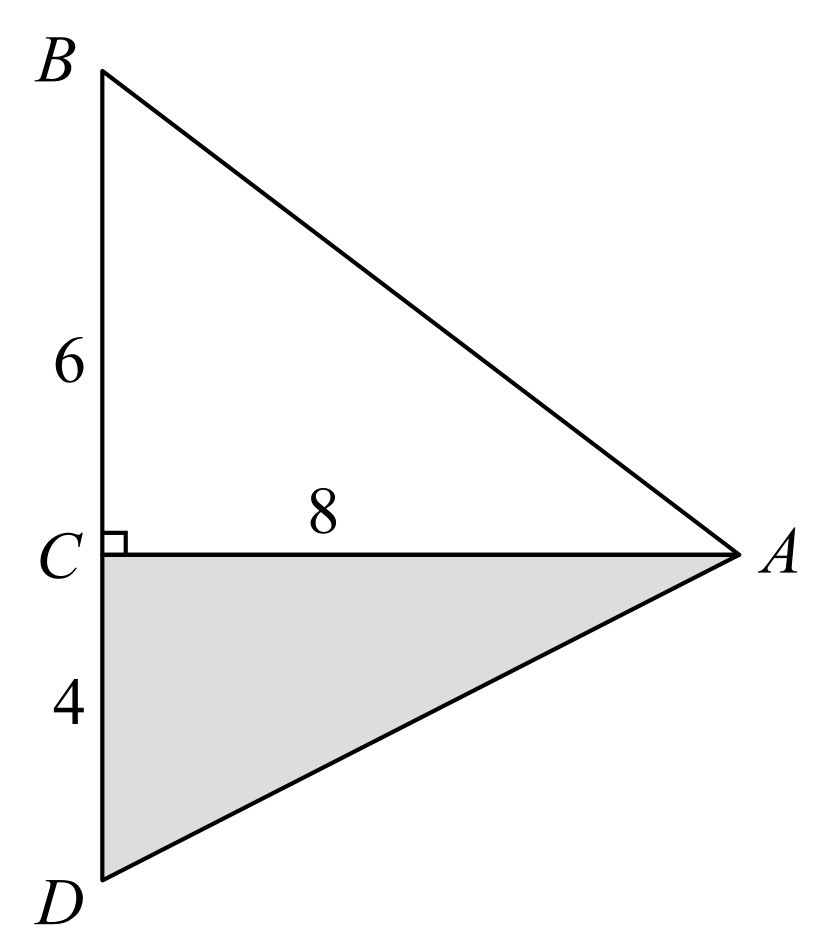
图1-2

③如图1-3所示，DA=DB，设CD=xm，则DA=（x+6）m，在Rt△ACD中，由勾股定理得x2+82=（x+6）2，解得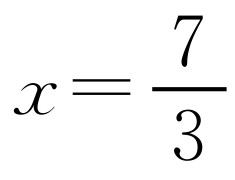.此时扩建后的等腰三角形花圃的.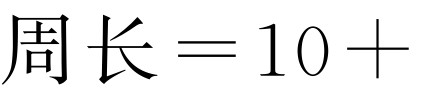

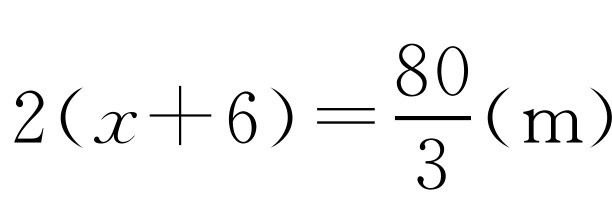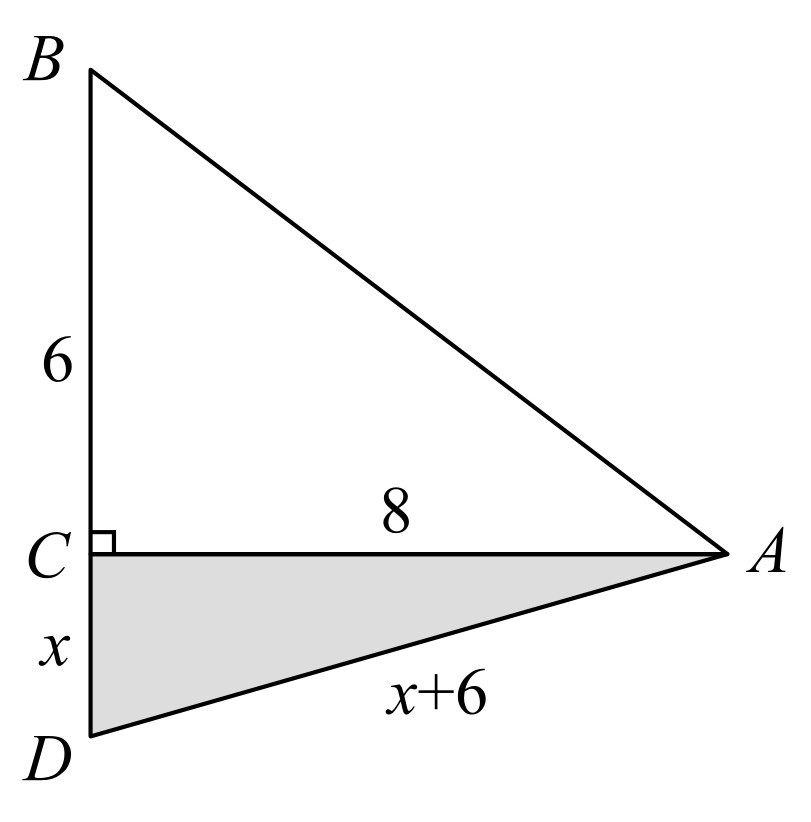
图1-3

综上，扩建后等腰三角形花圃的周长为32m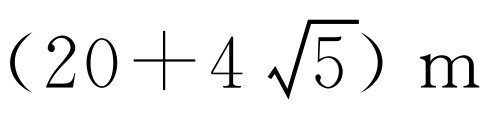或或.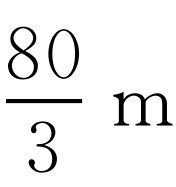

（☆☆☆）【1.4.2】

在△ABC中，AC=25，AB=35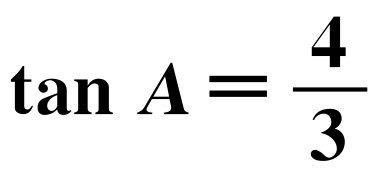，，点D为边AC上一点，且AD=5，点E，F分别为边AB上的动点（点F在点E的左边），且∠EDF=∠A．设AE=x，AF=y.

（1）如图1-4所示，当DF⊥AB时，求AE的长．

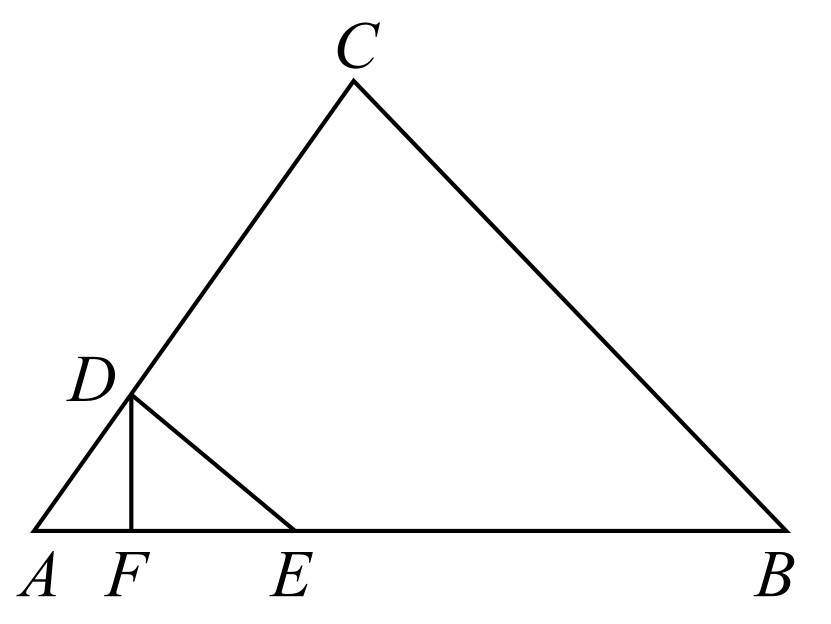
图1-4

（2）如图1-5所示，当点E，F在边AB上时，求y关于x的函数关系式，并写出函数的定义域．

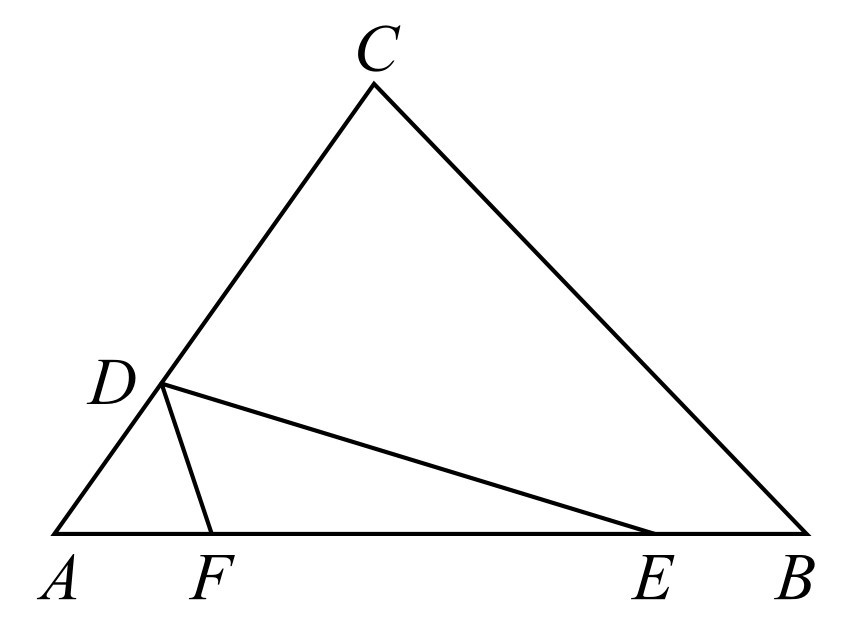
图1-5

（3）连接CE，当△DEC和△ADF相似时，求x的值．

【解析】

（1）因为DF⊥AB，所以∠AFD=90°，∠A+∠ADF=90°，

因为∠EDF=∠A，所以∠EDF+∠ADF=90°，

即∠ADE=90°，

在Rt△ADE中，∠ADE=90°，AD=5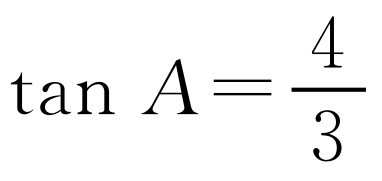，，所以.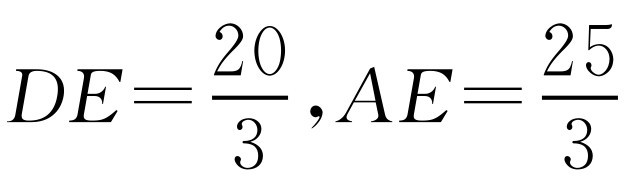

（2）如图1-6所示，过点D作DG⊥AB，交AB于G.

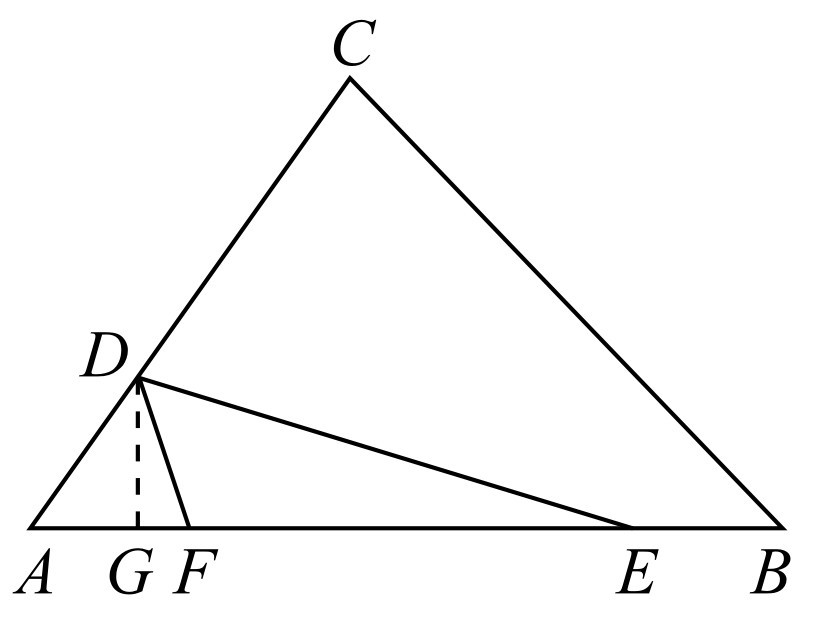
图1-6

因为∠EDF=∠DAE，∠DEF=∠AED，所以△EDF∽△EAD，所以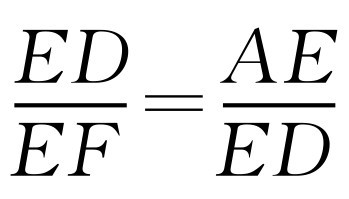，ED2=AE·EF，

因为Rt△AGD中，∠AGD=90°，AD=5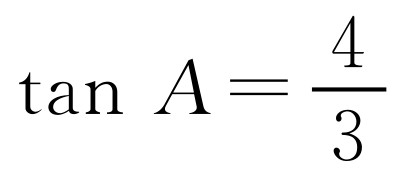，，所以DG=4，AG=3，所以EG=x-3，DE2=42+（x-3）2，所以42+（x-3）2=x·（x-y），所以.

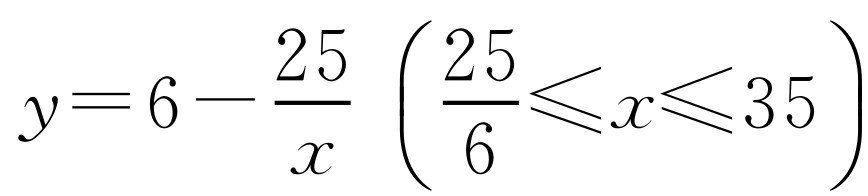（3）如图1-7所示，因为∠A+∠AFD=∠EDF+∠EDC，且∠EDF=∠A．所以∠ADF=∠EDC.

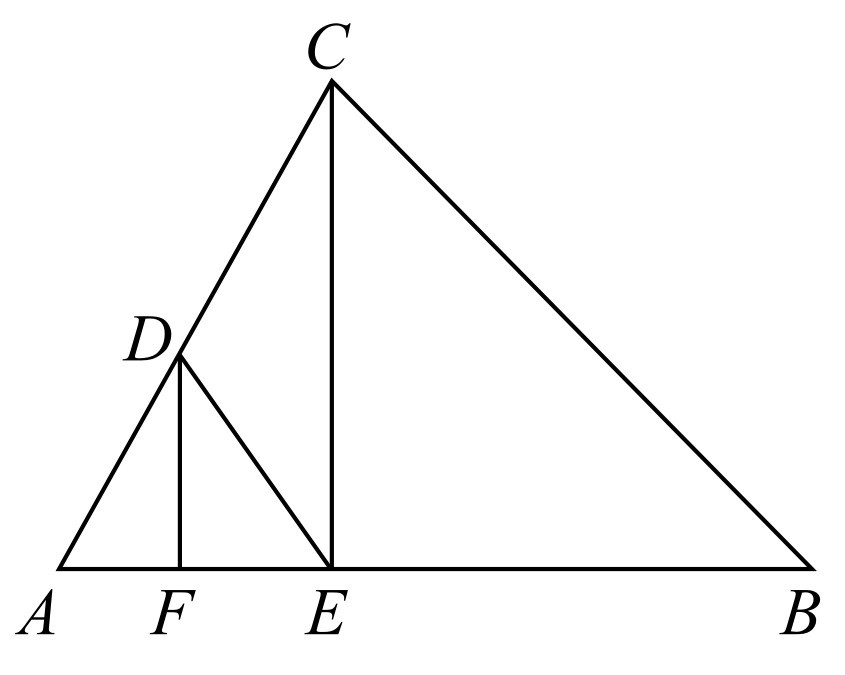
图1-7

①当∠A=∠CED时，

因为∠EDF=∠A，∠CED=∠FDE，所以DF∥CE，，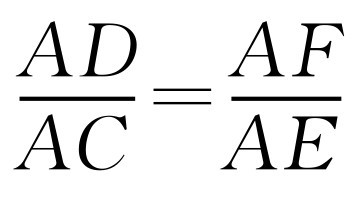

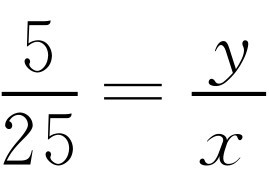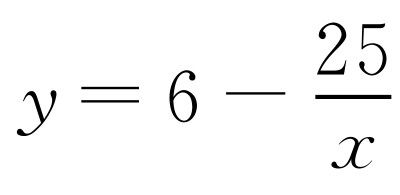所以，因为，所以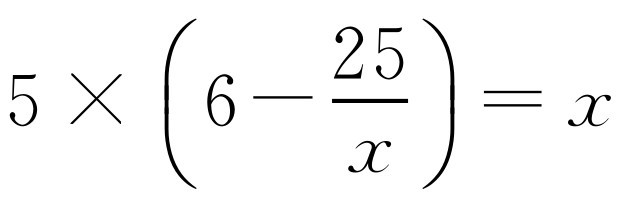，x1=25，x2=5.

②当∠A=∠DCE时，AE=CE=x

因为∠ADF=∠COE，所以△ECD∽△DAF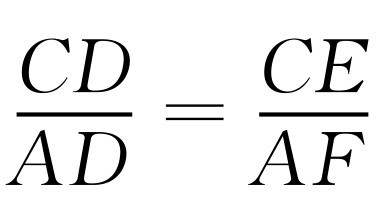，所以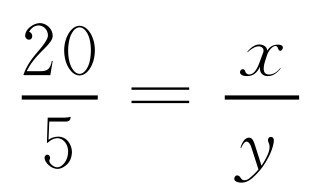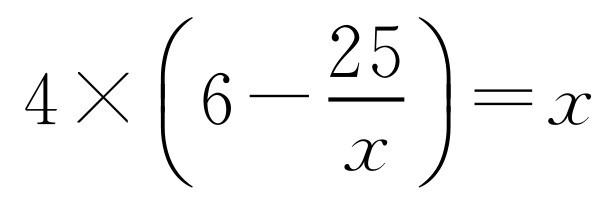，所以，，所以.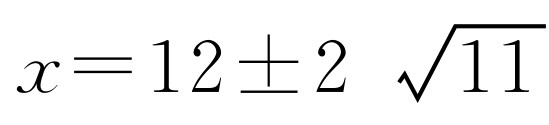

综上，当△DEC和△ADF相似时，x=25或x=5或.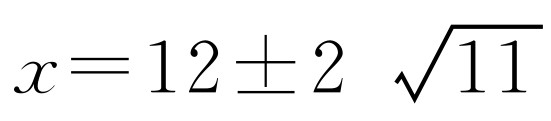

（☆☆☆）【1.4.3】

如图1-8所示，在Rt△ABC中，∠C=90°.翻折∠C，使点C落在斜边AB上某一点D处，折痕为EF（点E，F分别在边AC，BC上），若△CEF与△ABC相似，求：

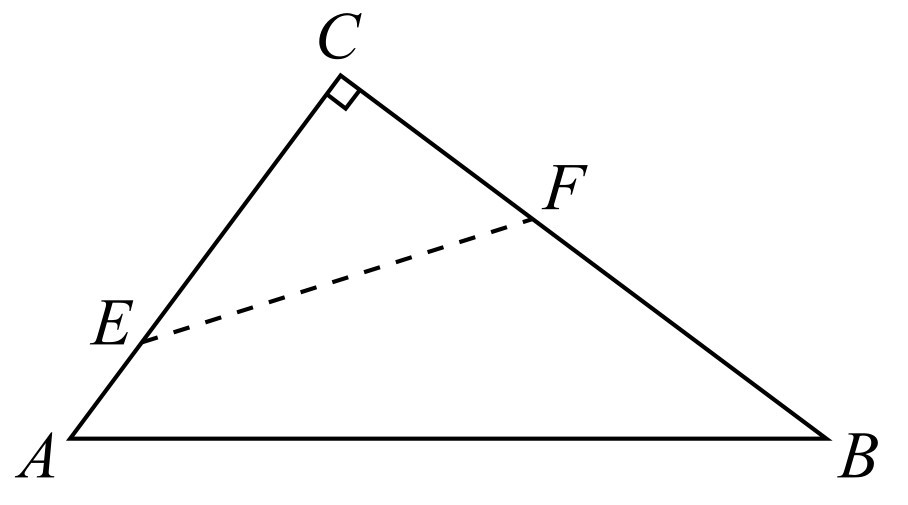
图1-8

（1）当AC=BC=2时，AD的长为________.

（2）当AC=3，BC=4时，AD的长为________.

【解析】

（1）当AC=BC=2时，△ABC为等腰直角三角形，如图1-9所示．

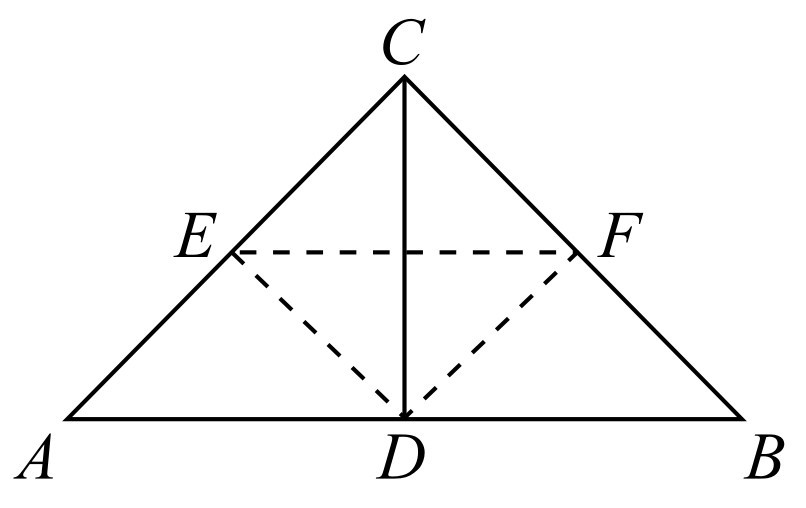
图1-9

此时D为AB边中点，.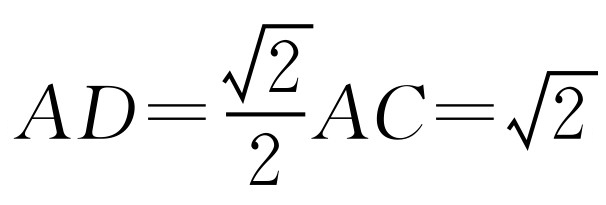

（2）当AC=3，BC=4时，有两种情况：

①若CE:CF=3:4，如图1-10所示．

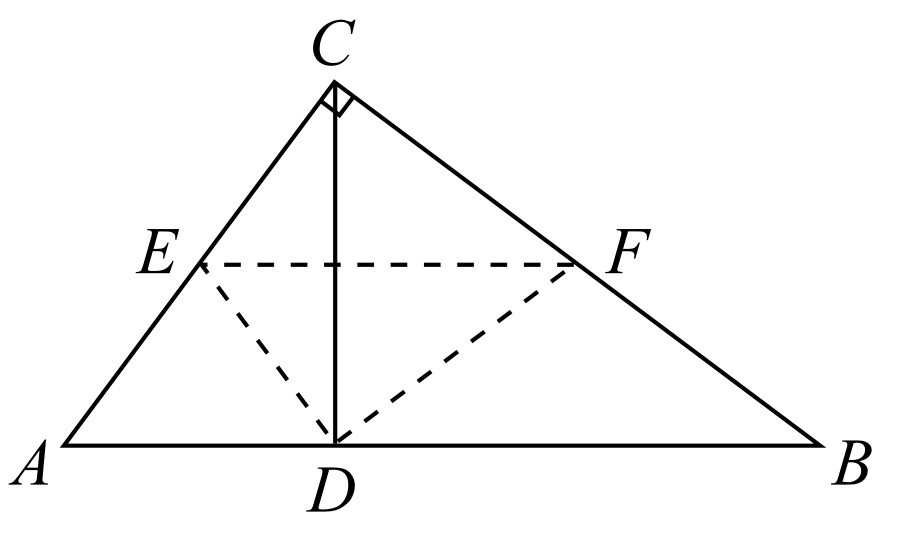
图1-10

因为CE:CF=AC:BC，

由折叠性质可知，CD⊥EF，所以CD⊥AB，即此刻CD为AB边上的高．

在Rt△ABC中，AC=3，BC=4，所以AB=5，，.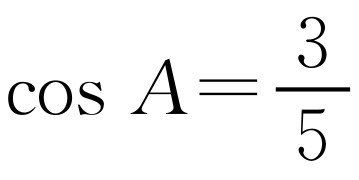

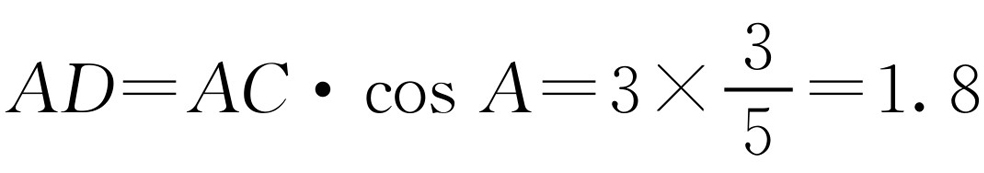②若CF:CE=3:4，如图1-11所示．

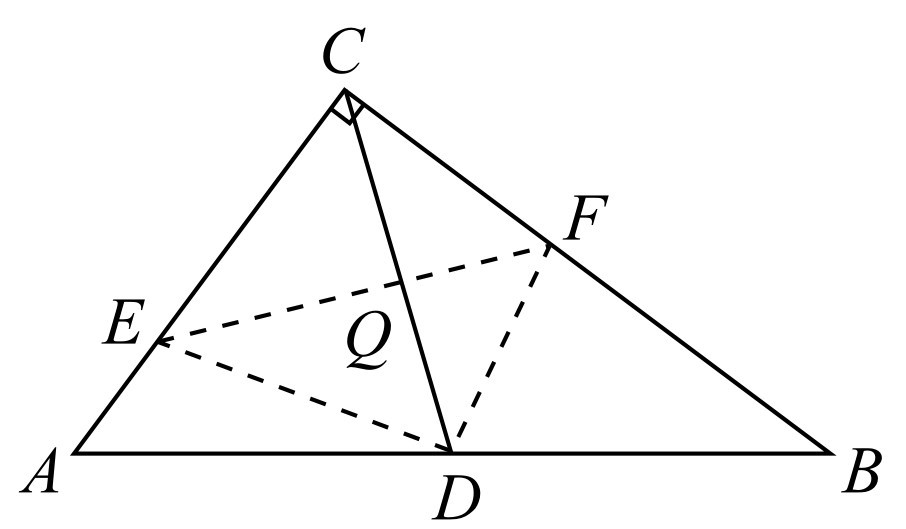
图1-11

因为△CEF与△ABC相似，所以∠CEF=∠B．由折叠性质可知，∠CEF+∠ECD=90°，又因为∠A+∠B=90°，所以∠A=∠ECD，AD=CD.

同理可得∠B=∠FCD，CD=BD.

从而.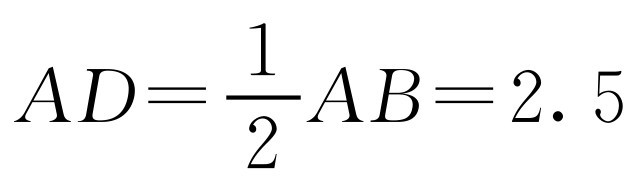

综上，当AC=3，BC=4时，AD的长为1.8或2.5.

（☆☆）【巩固练习4】