【典型应用2】几何相关
（☆）【2.2.1】
如图2-1所示，是一个照相机成像的示意图．
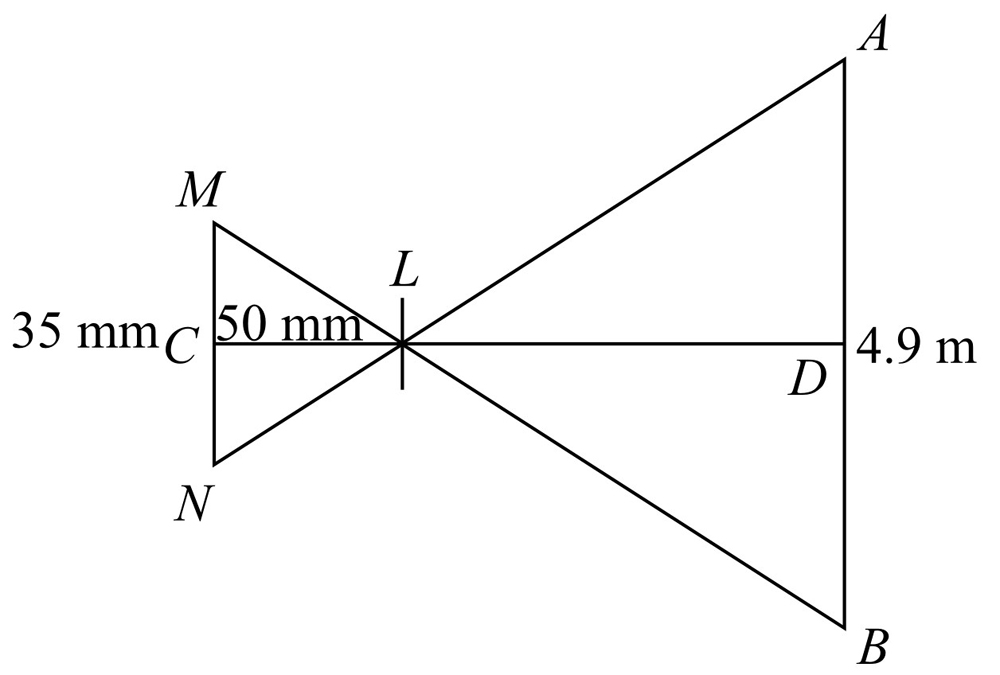
图2-1
（1）如果像高MN是35mm，焦距是50mm，拍摄的景物高度AB是4.9m，拍摄点离景物有多远？
（2）如果要完整的拍摄高度是2m的景物，拍摄点离景物有4m，像高不变，则相机的焦距应调整为多少？
【解析】
根据物体成像原理知：△LMN∽△LBA，得到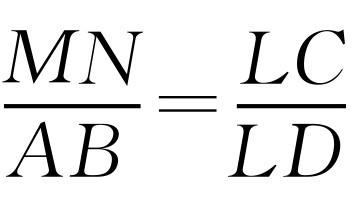
.
（1）由题意，像高MN是35mm，焦距是50mm，拍摄的景物高度AB是4.9m，解得LD=7，因此拍摄点距景物7m；
（2）拍摄高度是2m的景物，拍摄点离景物有4m，像高不变，解得LC=70，因此相机的焦距应调整为70mm.
（☆☆）【2.2.2】
王大伯要做一张如图2-2所示的梯子，梯子共有7级互相平行的踏板，每相邻两级踏板之间的距离都相等．已知梯子最上面一级踏板的长度A1B1=0.5m，最下面一级踏板的长度A7B7=0.8m．则第5级踏板的长度为（ ）.
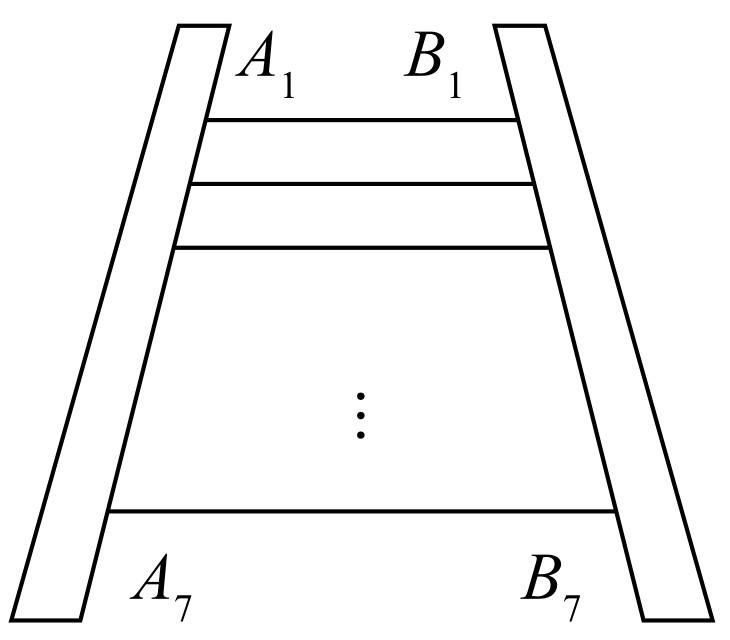
图2-2
A．0.6m
B．0.65m
C．0.7m
D．0.75m
【解析】
因为每相邻两级踏板之间的距离都相等，所以A4B4为梯形A1A7B7B1的中位线，根据梯形中位线定理，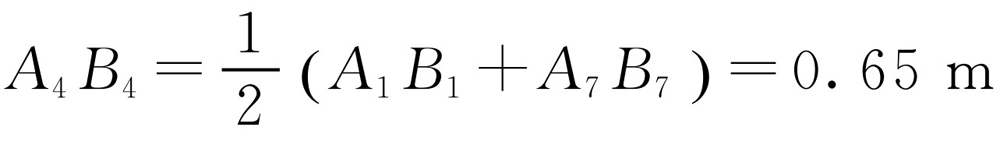
．如图2-3所示，作A1C∥B1B4并延长AC交A5B5于点D，则DB5=CB4=A1B1=0.5m，A4C=0.65-0.5=0.15m，于是
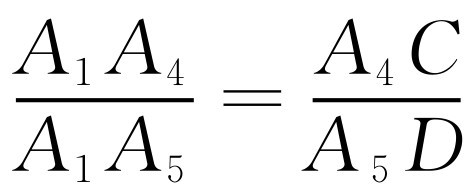解得A5D=0.2m.A5B5=0.2+0.5=0.7m.
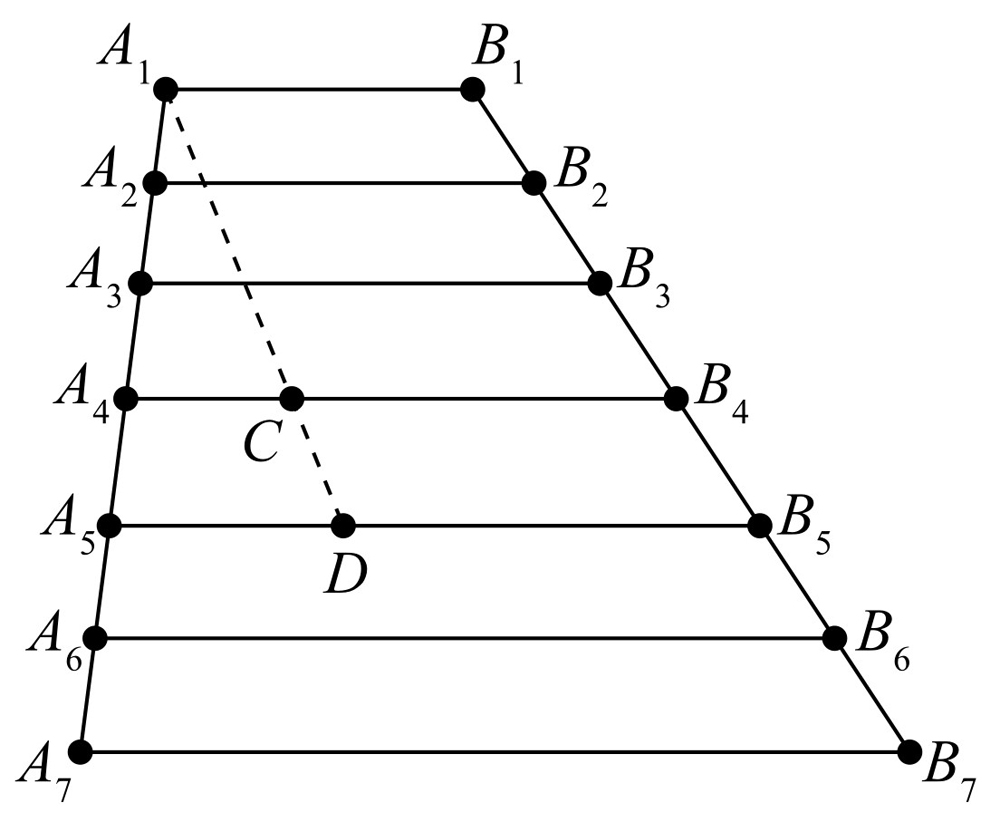
图2-3
故选C.
（☆☆）【2.2.3】
如图2-4所示，港口B位于港口D正西方向120海里处，小岛C位于港口D北偏西60°的方向上，一艘科学考察船从港口D出发，沿北偏西30°的DA方向以每小时20海里的速度驶离港口D，同时一艘快艇从港口B出发沿北偏东30°的方向以每小时60海里的速度驶向小岛C．在小岛C处用1小时装补给物质后，立即按原来的速度给考察船送去．
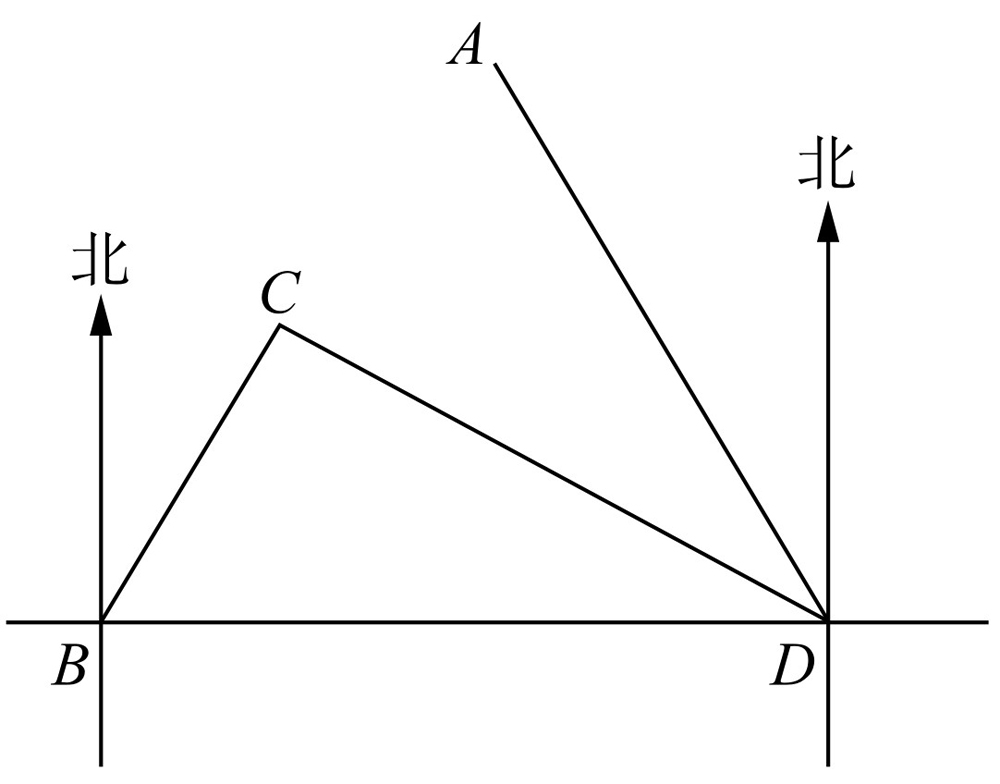
图2-4
（1）快艇从港口B到小岛C需要多少时间？
（2）快艇从小岛C出发后最少需要多少时间才能和考察船相遇？
【解析】
（1）由题意∠BCD=90°，BC=60，所以快艇到达C处的时间：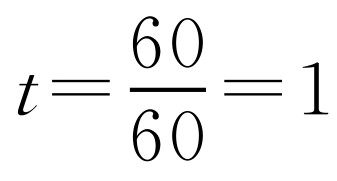
（小时）.
（2）如图2-5所示，作CF⊥DA于点F，因为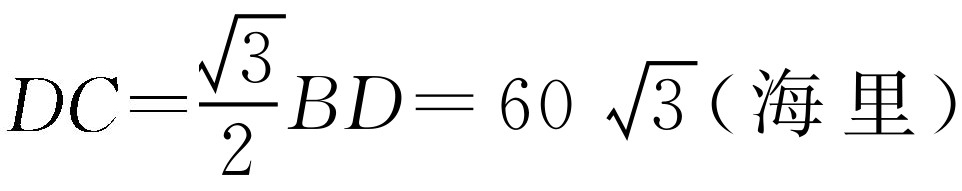
，所以在Rt△CDF中，∠CDF=30°．所以
（海里）．所以
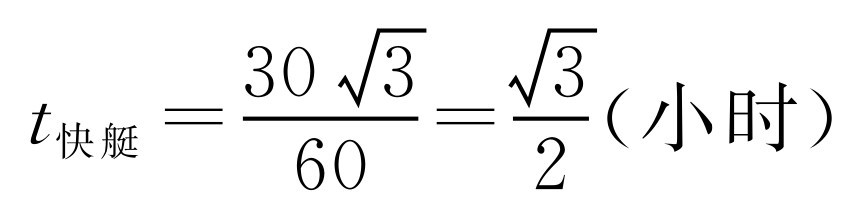，而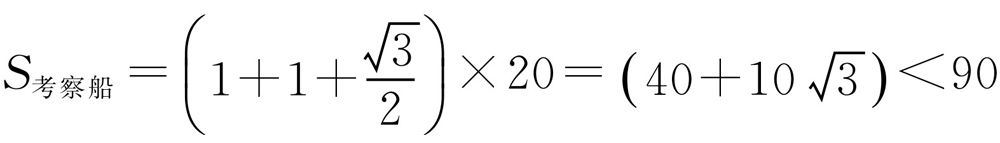
.所以两船不可能在点F处相遇．
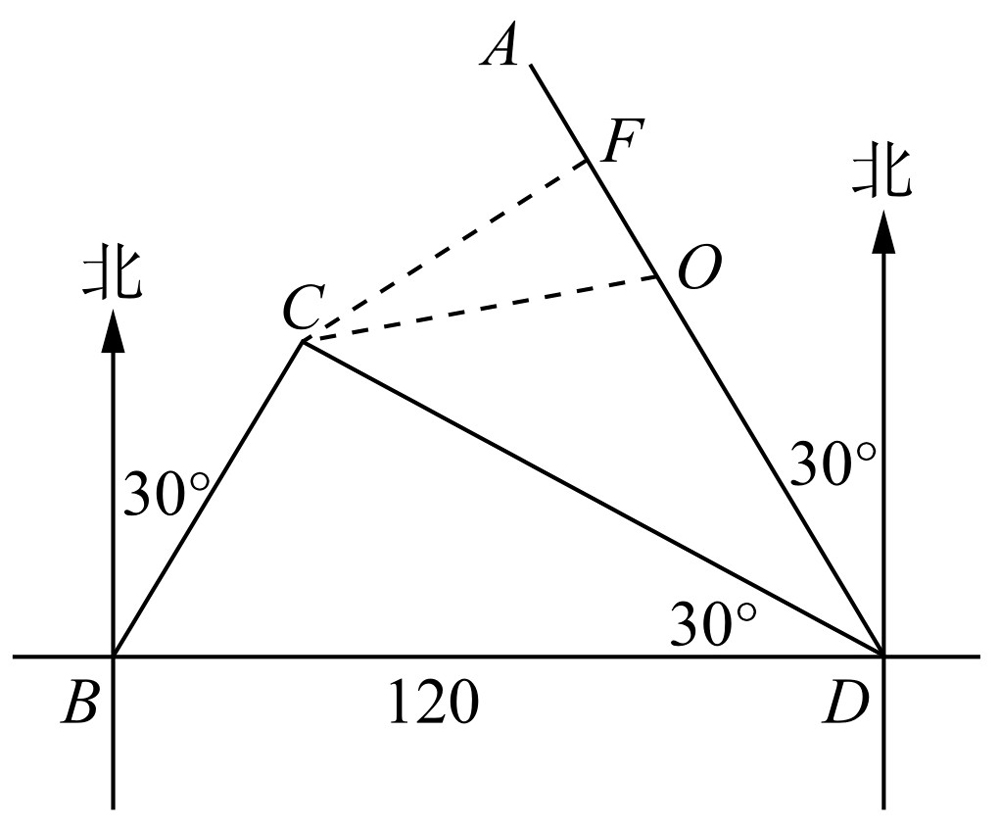
图2-5
假如两船在点O处（点O在DF之间）相遇，设快艇从小岛C出发后最少需x小时与考察船相遇，相遇时考察船共用了（x+2）小时，所以OD=20（x+2），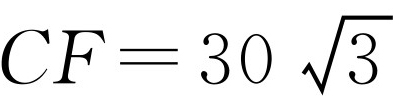
.所以OF=DF-OD=90-20x-40=50-2x，CO=60x．在Rt△COF中，由勾股定理CF2+FO2=CO2，即
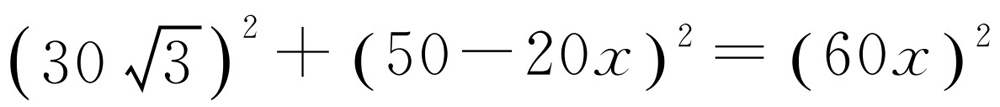，整理得8x2+5x-13=0，解得x1=1，
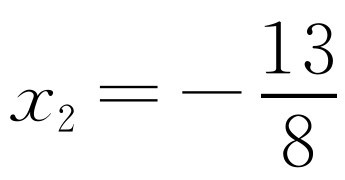（不合题意，舍去）.
综上，快艇从小岛C出发后最少需要1小时才能和考察船相遇．
（☆☆）【巩固练习2】
在同一时刻两根木杆在太阳光下的影子如图2-6所示，其中木杆AB=2m，它的影子BC=1.6m，木杆PQ的影子有一部分落在了墙上，PM=1.2m，MN=0.8m，则木杆PQ的长度为________ m.
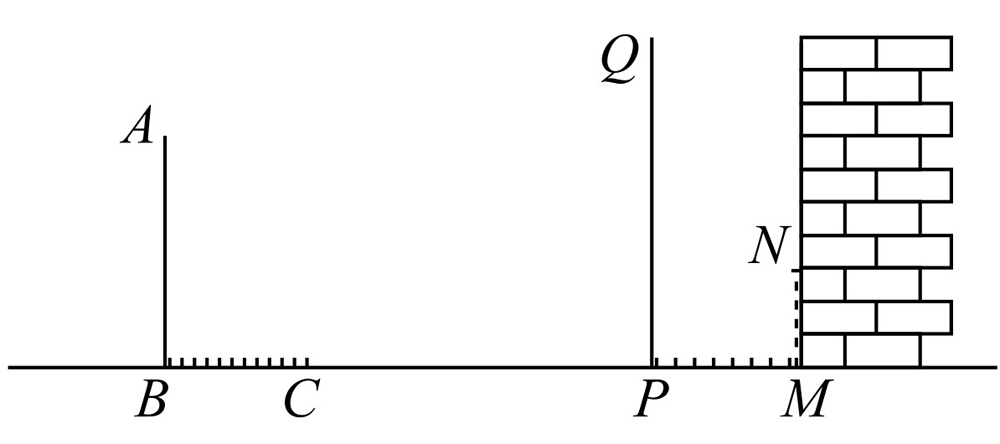
图2-6