【典型应用3】函数相关
（☆☆）【2.3.1】
如图2-7所示是一个横断面为抛物线形状的拱桥，当水面宽4m时，拱顶（拱桥洞的最高点）离水面2m，水面下降1m时，水面的宽度为________ m.
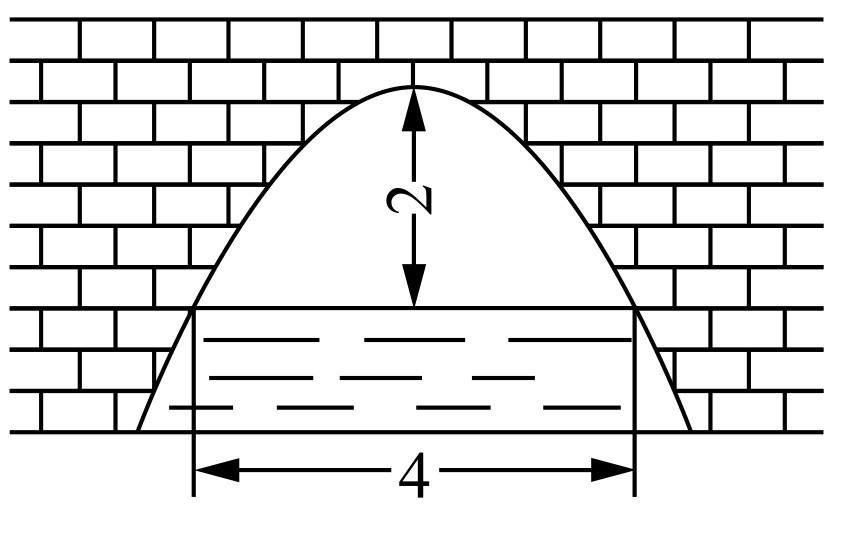
图2-7
【解析】
如图2-8所示，建立平面直角坐标系，设横轴x通过AB，纵轴y通过AB中点O且通过点C，则通过画图可得知O为原点．
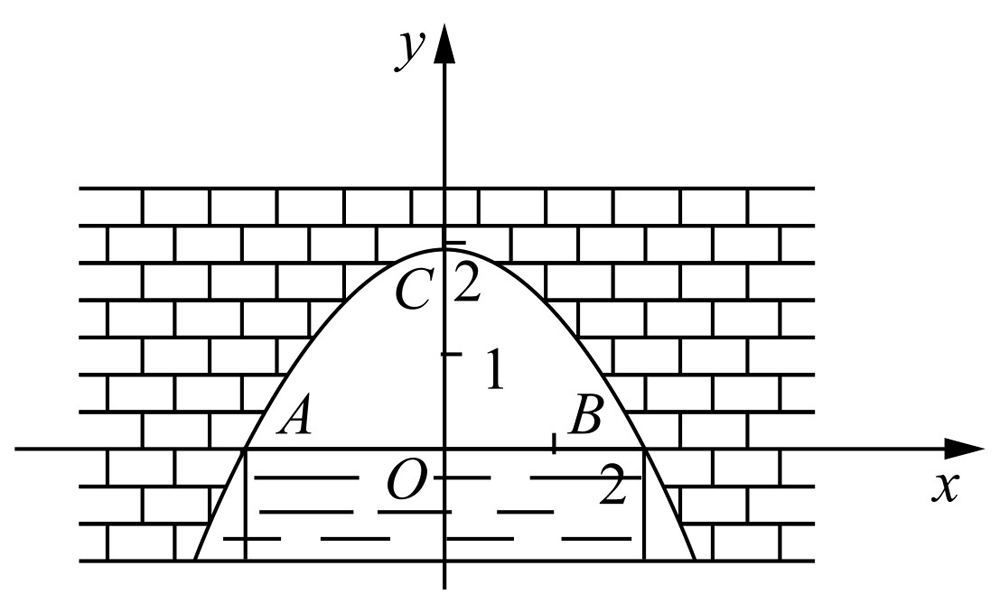
图2-8
抛物线以y轴为对称轴，且经过A，B两点，抛物线顶点C坐标为（0，2），通过以上条件可设顶点式y=ax2+2，其中a可通过代入A点坐标（-2，0）到抛物线解析式得出：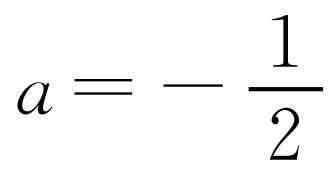
，所以抛物线解析式为
，
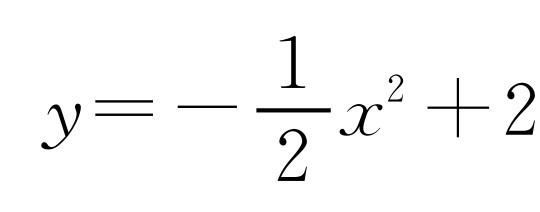当水面下降1m，通过抛物线在图上的观察可转化为：当y=-1时对应的抛物线上两点之间的距离，也就是直线y=-1与抛物线相交的两点之间的距离，可以通过把y=-1代入抛物线方程，解得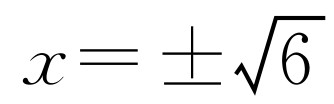
，所以水面宽度增加到
.
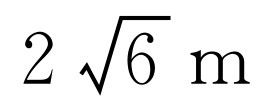（☆☆）【2.3.2】
科学家为了推测最适合某种珍奇植物生长的温度，将这种植物分别放在不同温度的环境中，经过一段时间后，测试出这种植物高度的增长情况，部分数据如表：
科学家经过猜想、推测出l与t之间是二次函数关系．由此可以推测最适合这种植物生长的温度为________℃.
【解析】
设y=ax2+bx+c（a≠0），将（0，49），（1，46），（4，25）代入后解得：a=-1，b=-2，c=49．得函数解析式为y=-x2-2x+49，当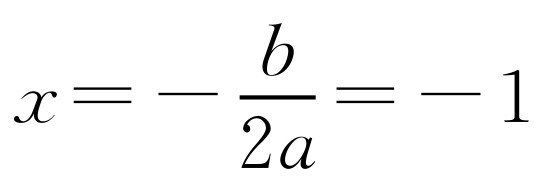
时，y有最大值50，即说明最适合这种植物生长的温度是-1℃.
（☆☆）【巩固练习3】
如图2-9所示，已知点A在反比例函数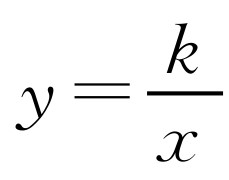
的图像上，点B在x轴的正半轴上，且△OAB是面积为
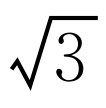的等边三角形，那么这个反比例函数的解析式是________.
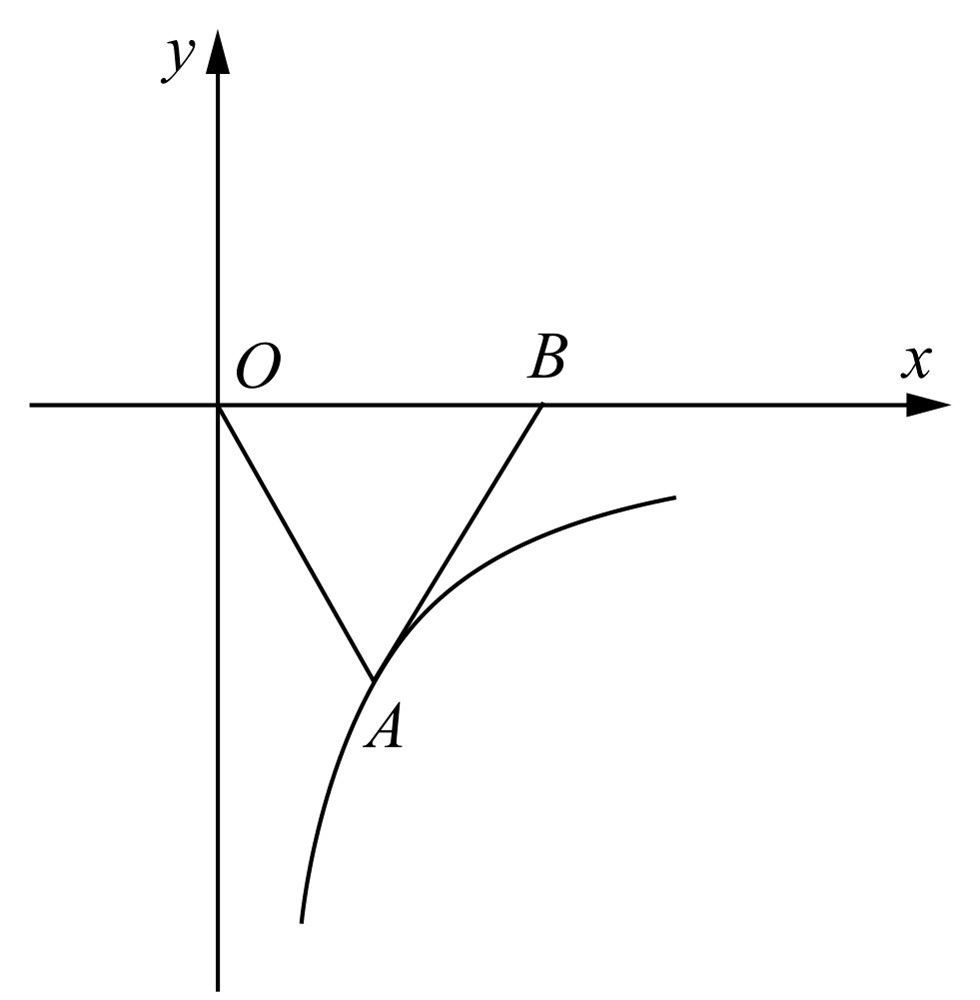
图2-9