【典型应用3】绝对值
(☆)【1.3.1】
解方程|x-1|+|x+2|=5.
【解析】
令x-1=0,x+2=0,解得x=1,x=-2,可以分成以下3种情况:
(1)当x<-2时,-(x-1)-(x+2)=5,解得x=-3,符合x<-2;
(2)当-2≤x<1时,-(x-1)+(x+2)=5,此方程无解;
(3)当x≥1时,(x-1)+(x+2)=5,解得x=2,符合x≥1.
(☆☆)【1.3.2】
已知a,b,c,d都是整数,且|a+b|+|b+c|+|c+d|+|d+a|=2,求|a+d|的值.
【解析】
由题意得:|a+b|,|b+c|,|c+d|,|d+a|是整数,所以有两种可能:①3个绝对值为0,1个绝对值为2;②2个绝对值为0,2个绝对值为1.所以|d+a|只可能取0,1,2.
①若|a+d|=2,则|a+b|=|b+c|=|c+d|=0,则a=-d,所以|a+d|=0,与假设|a+d|=2矛盾.
②若|a+d|=1,a=0,b=0,c=-1,d=1,此时|a+d|=1;
③若|a+d|=0,a=-1,b=0,c=0,d=1,此时|a+d|=0.
综上,|a+d|的值为1或0.
(☆☆☆)【1.3.3】
a,b,c均为整数,且|a-b|2012+|c-a|2013=1,试求(c-a)2012+|a-b|+|b-c|2013的值.
【解析】
由a,b,c均为整数,|a-b|2012+|c-a|2013=1可知,只能是0+1=1或1+0=1.
①当|a-b|=0,|c-a|=1时,原式=1+0+1=2;
②当|a-b|=1,|c-a|=0时,原式=0+1+1=2.
综上,所求式的值为2.
(☆☆)【巩固练习3】
已知a,b,c为不等于零的有理数,求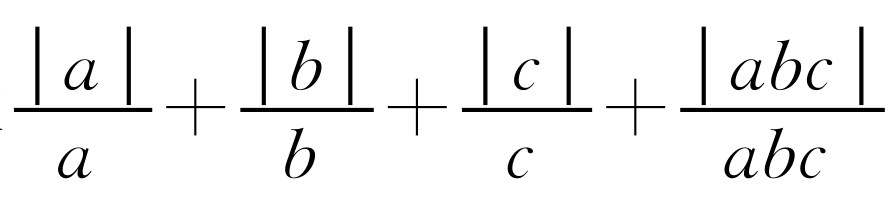 的值.
的值.