【典型应用3】函数相关
(☆)【28.3.1】
已知二次函数y=ax2+bx+c的图像与x轴交于点(-2,0),(x1,0),且1<x1<2.与y轴的正半轴的交点在点(0,2)的下方,则下列结论①a<b<0;②2a+c>0;③4a+c<0;④2a-b+1>0中正确的是________.(写出序号)
【解析】
设x1=1.5,与y轴交于(0,1),那么这个二次函数的解析式就可以用待定系数法解出来.于是就可以用具体的a,b,c的值进行判断.故选②③.
(☆☆)【28.3.2】
已知关于x的一次函数y=ax-a+1和y=(a-1)x-a+2,它们的图像交点是________.
【解析】
a的变化并不影响交点.不妨取a=2,可得方程组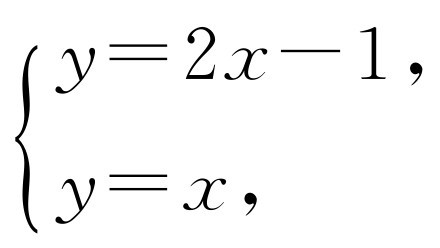 所以
所以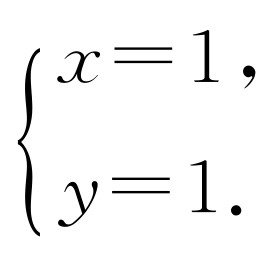 故交点为(1,1).
故交点为(1,1).
(☆☆)【28.3.3】
如果方程(x2-2x+m)(x-1)=0的三根可作为一个三角形的三边长,则m的取值范围是( ).
A.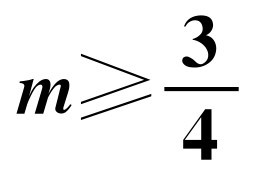
B.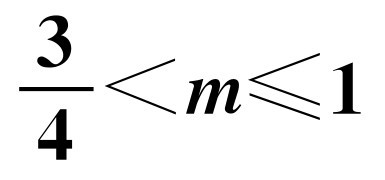
C.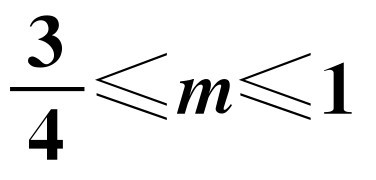
D.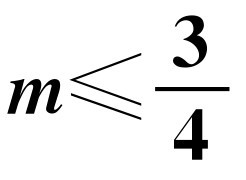
【解析】
根据选项,不妨取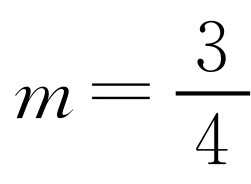 ,代入方程得
,代入方程得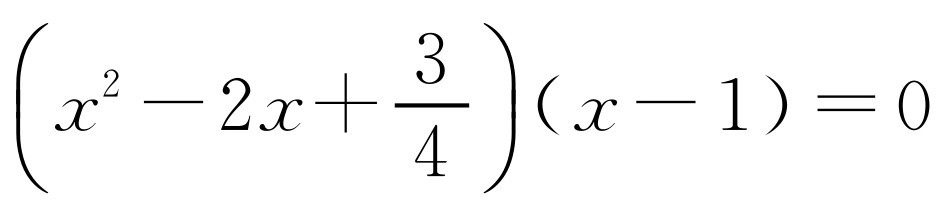 ,解得
,解得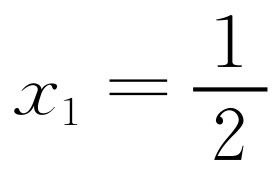 ,
,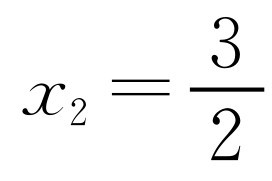 ,x3=1.所以x1+x3=x2,所以不符合三角形两边之和大于第三边.故选B.
,x3=1.所以x1+x3=x2,所以不符合三角形两边之和大于第三边.故选B.
(☆☆)【巩固练习3】
若a,b为定值,且无论k取何值时,关于x的一次方程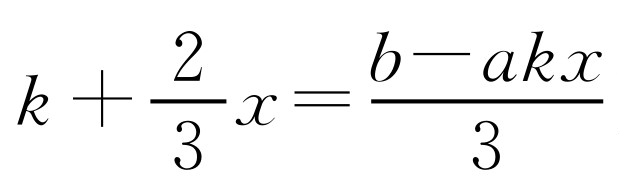 的解总是-1,求a,b的值.
的解总是-1,求a,b的值.