【典型应用2】几何相关
(☆☆☆)【28.2.1】
如图28-1所示,已知矩形ABCD,以C为圆心,CA为半径画圆弧分别交AB,AD延长线于点E和点F,连接EB,FD,若把直角∠BCD绕点C旋转角度θ(0°<θ<90°),使得该角的两边分别交线段AE和AF于点P和点Q,则CQ2+CP2等于( ).
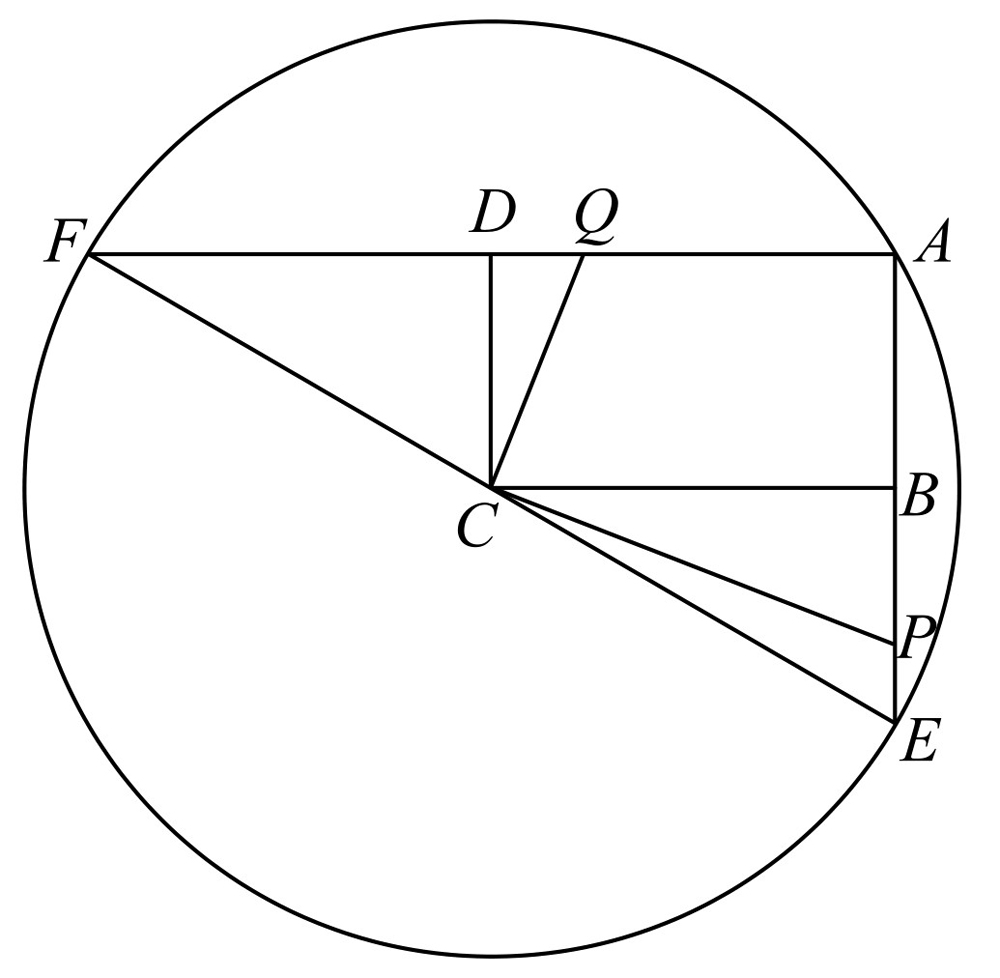
图28-1
A.2QF·PE
B.QF2+PE2
C.(QF+PE)2
D.QF2+PE2+QF·PE
【解析】
令θ=0°,如图28-2所示,此时Q与D重合,P与B重合,由于△FDC≌△CBE,FD=CB,DC=BE,故CQ2+CP2=CD2+CB2=QF2+PE2,选B.
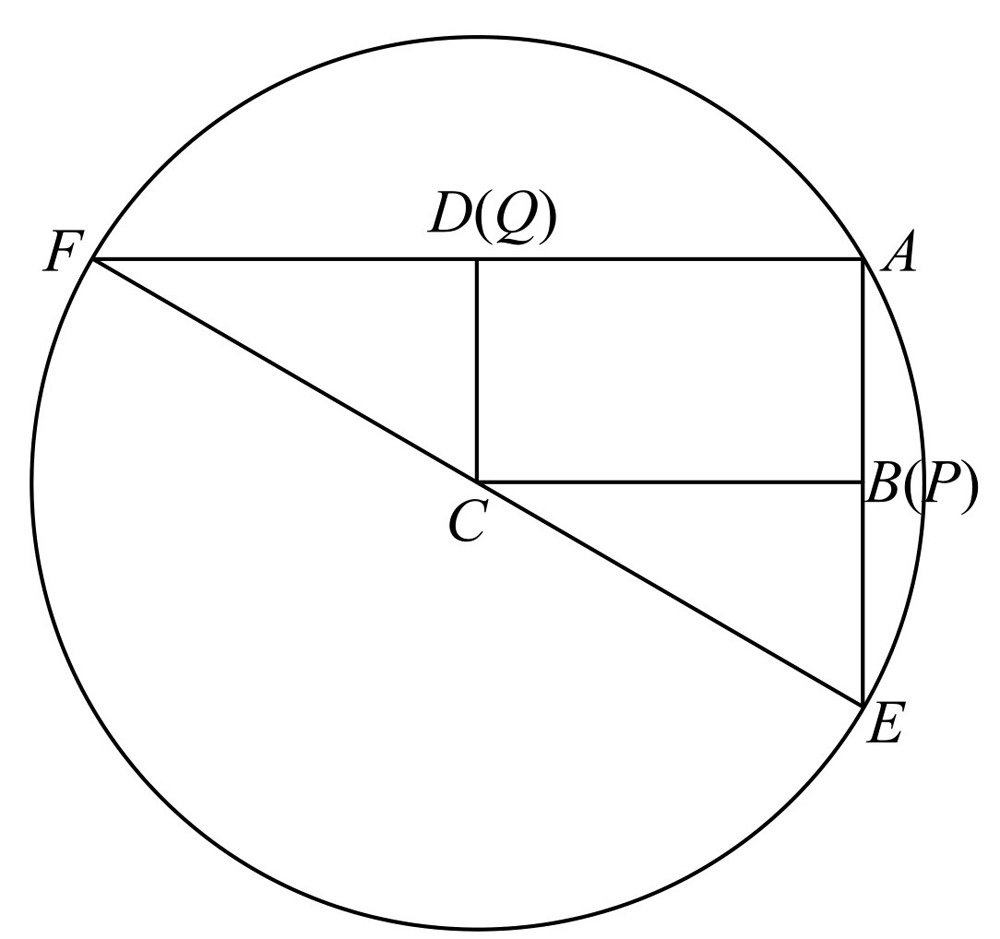
图28-2
(☆☆☆)【28.2.2】
如图28-3所示,点E是平行四边形ABCD对角线AC上任一点,则下列结论正确的是( ).
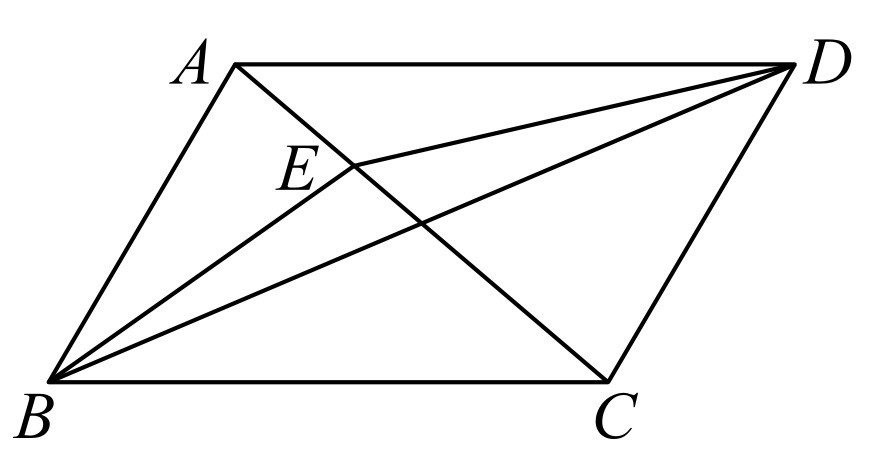
图28-3
A.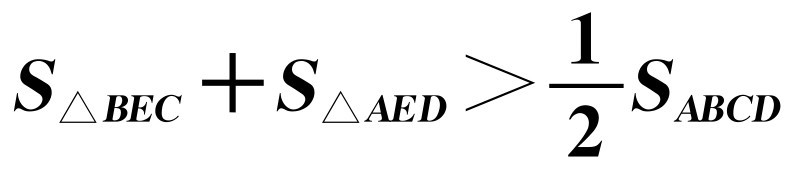
B.S△BEC=S△DEC
【解析】
因为E是AC上的任意一点,设E是AC的中点,则B,D,E三点共线,那么C点到BE的距离与C点到DE的距离相等,从而可知,S△BEC=S△DEC,故选B.
(☆☆☆)【28.2.3】
如图28-4所示,正方形ABCD的边长为1,其对角线BD上一点E,且BE=BC,P为CE上任一点,作PQ⊥BC于点Q,PR⊥BE于R,则PQ+PR的值为( ).
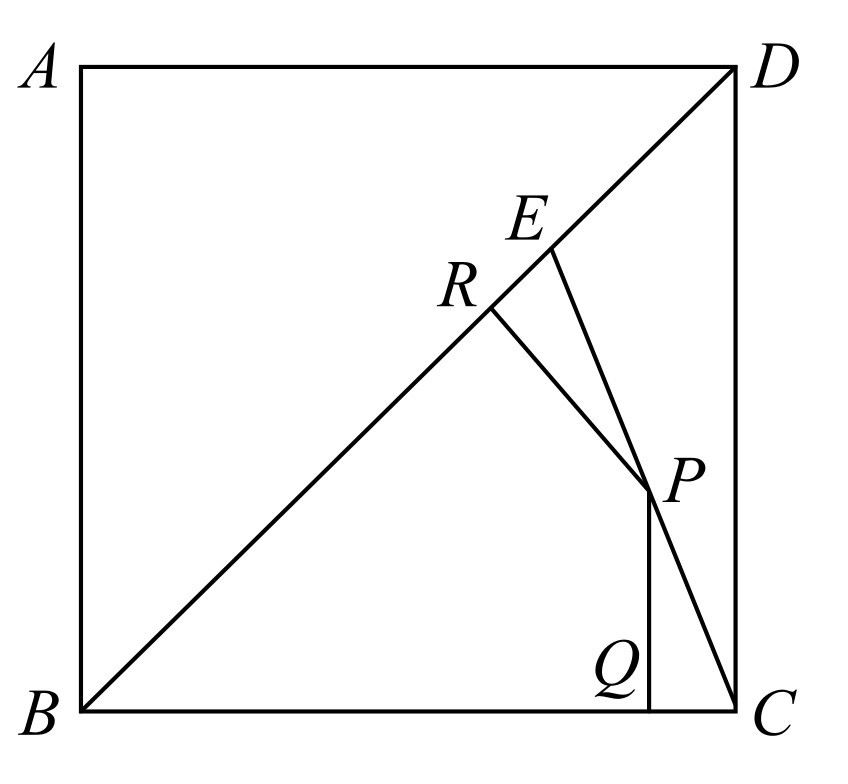
图28-4
A.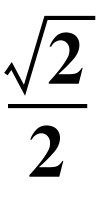
B.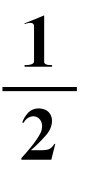
C.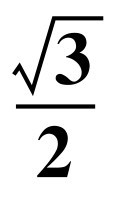
D.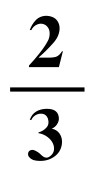
【解析】
当点P与点E重合时,因BE=BC=1,故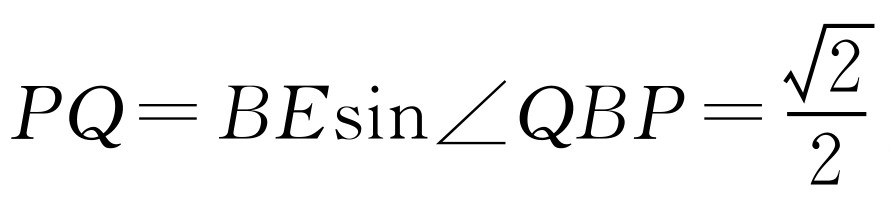 ,所以
,所以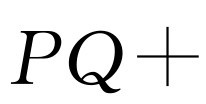
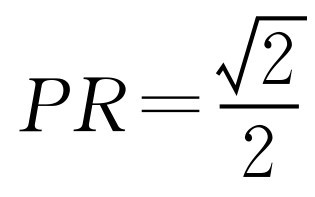 ,故选A.
,故选A.
(☆☆)【巩固练习2】
如图28-5所示,以OA为斜边作等腰直角△OAB,再以OB为斜边在△OAB外侧作等腰直角△OBC,依此类推,得到8个等腰直角三角形,求△OAB与△OHI的面积比值.
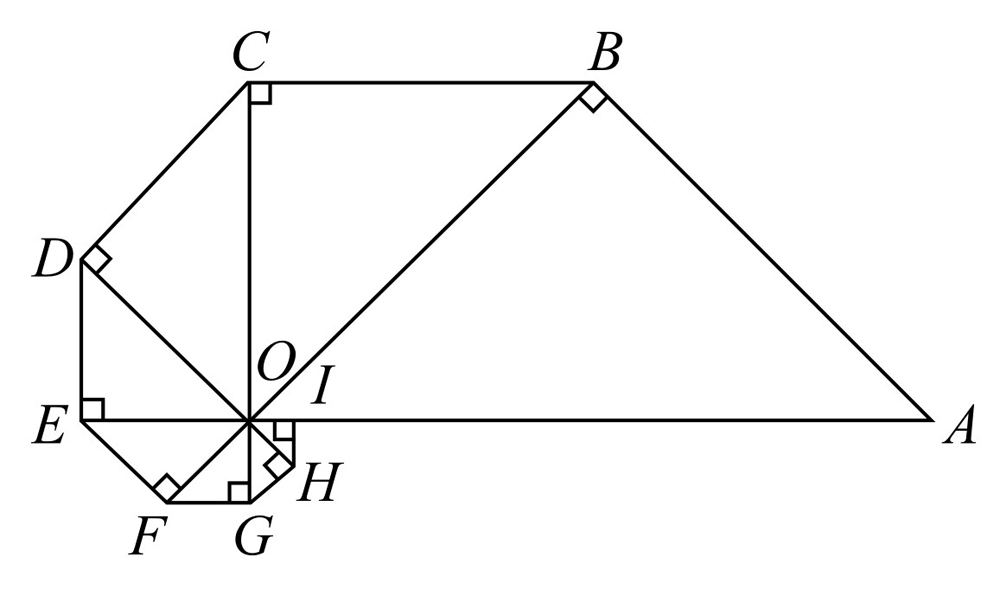
图28-5