【典型应用2】整式除法
(☆☆)【24.2.1】
当m,n为何值时,多项式x4-5x3+11x2+mx+n能被x2-2x+1整除?
【解析】
设商式为x2+px+n,所以
x4-5x3+11x2+mx+n=(x2+px+n)(x2-2x+1)=x4+(p-2)x3+(n-2p+1)x2+(p-2n)x+n
由各对应项的系数相等,解得m=-11,n=4.
(☆☆)【24.2.2】
若3x3+hx2-5x+k恰好能被x+3整除,被x+1除余数为4,求h,k,并将多项式3x3+hx2-5x+k进行因式分解.
【解析】
记f(x)=3x3+hx2-5x+k,则 代入得
代入得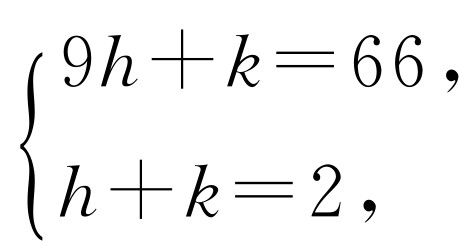 解得h=8,k=-6.所以f(x)=3x3+8x2-5x-6,由于f(x)必有因式x+3,设其商式为ax2+bx+c,比较系数可以得到f(x)=(x+3)(ax2+bx+c)=3x3+8x2-5x-6,
解得h=8,k=-6.所以f(x)=3x3+8x2-5x-6,由于f(x)必有因式x+3,设其商式为ax2+bx+c,比较系数可以得到f(x)=(x+3)(ax2+bx+c)=3x3+8x2-5x-6,

所以f(x)=(x+3)(3x2-x-2)=(x+3)(x-1)(3x+2).
(☆☆☆)【24.2.3】
已知多项式x3+bx2+cx+d的系数都是整数.若bd+cd是奇数,求证:这个多项式不能分解成两个整系数多项式的乘积.
【解析】
假设原多项式可以分解因式,设
x3+bx2+cx+d=(x+m)(x2+nx+r) ①,
m,n,r都是整数,比较系数得mr=d,因为bd+cd=d(b+c)是奇数,那么d=mr,b+c也为奇数,可见m,r也都是奇数.
在式①中,令x=1,得1+b+c+d=(1+m)(1+n+r).左边因为b+c,d=mr都是奇数,故1+b+c+d是奇数;右边因为m为奇数,故m+1为偶数,因此右边为偶数.
显然,奇数≠偶数,原假设不成立.因此题中的多项式不能分解为两个整系数多项式的乘积.
(☆☆☆)【巩固练习2】
将分式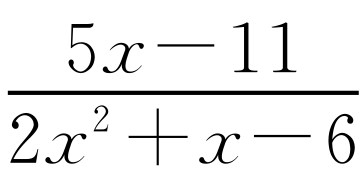 分解为部分分式(类似于将有理分数分解成许多次数较低有理分数和的形式).
分解为部分分式(类似于将有理分数分解成许多次数较低有理分数和的形式).