初中数学代数专题22奇偶分析法【典型应用1】化简求值

【典型应用1】化简求值

（☆☆）【22.1.1】

代数式ruz-rwy-suz+swx+tvy-tvx中，r，s，t，u，v，w，x，y，z可以分别取1或-1.

（1）求证：该代数式的值都是偶数．

（2）求该代数式所能取到的最大值．

【解析】

（1）由题意，代数式ruz-rwy-suz+swx+tvy-tvx的每一个加项由题设知只能取值1或-1，又因为偶数个奇数相加减，结果为偶数，所以该代数式的值都是偶数．

（2）因为ruz，-rwy，-suz，swx，tvy，-tvx的积为-（rstuvwxyz）2=-1，所以代数式ruz，-rwy，-suz，swx，tvy，-tvx中-1的个数是奇数，最少有1个，所以该代数式所能取到的最大值为1×5+（-1）=4.

（☆☆☆）【22.1.2】

设k（k≥3）是给定的正整数，是否存在正整数m，n，使得m（m+k）=n（n+1）成立．

【解析】

当k=3时，易证得上式不可能成立．

当k≥4时，若k=2t（t是不小于2的整数）为偶数，取m=t2-t，n=t2-1则m（m+k）=t4-t2，n（n+1）=t4-t2，因此这样的m，n满足条件．

若k=2t+1（t是不小于2的整数）为奇数，取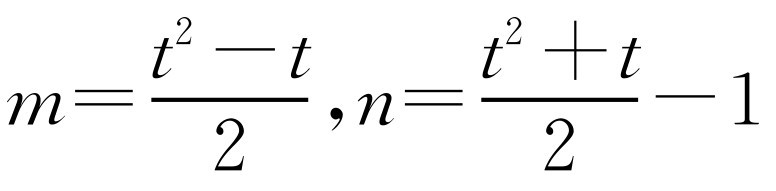，则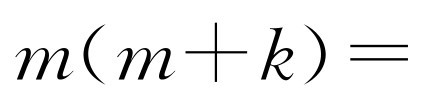，因此这样的m，n满足条件．综上所述，当k=3时，答案是否定的；当k≥4时，答案是肯定的．

（☆☆☆）【22.1.3】

若n是正整数，那么的值是________数（填“奇”或“偶”）.

【解析】

当n是偶数时，是偶数；

当n是奇数时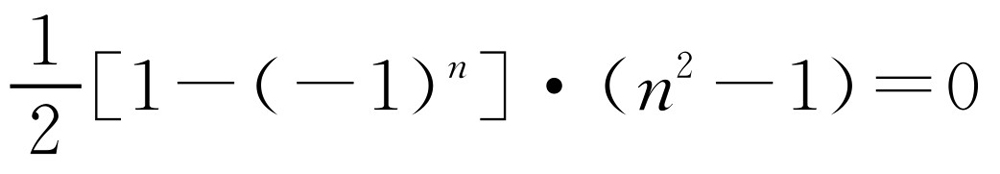，是偶数，故答案为偶数．

（☆☆☆）【22.1.4】

任意交换某个三位数的数字顺序得到一个新的三位数，原三位数与新三位数之和能否等于999？

【解析】

两数和为999，各位数相加时必定没有向上进位，又因为新三位数与原三位数只是三个数字的排列顺序不同，所以把两个三位数的个位、十位、百位数字加在一起一定是偶数，而9+9+9=27是奇数，矛盾．所以不能．

（☆☆）【巩固练习1】