【典型应用4】综合应用
（☆☆）【16.4.1】
二次函数y=ax2+bx+c的图像在x轴的下方，则所要满足的条件是（ ）.
A．a＜0，b2-4ac＜0
B．a＜0，b2-4ac＞0
C．a＞0，b2-4ac＜0
D．a＞0，b2-4ac＞0
【解析】
图像在x轴的下方，即a＜0．由于方程与x轴没有交点，即所对应二次方程没有解，故Δ=b2-4ac＜0，故选A.
（☆☆）【16.4.2】
若关于x的不等式组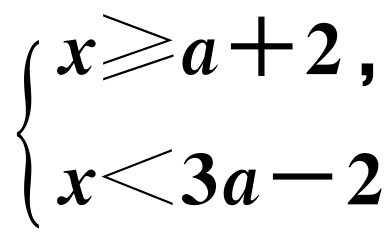
有解，求函数
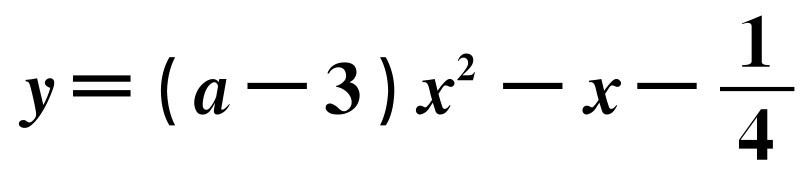的图像与x轴的交点个数．
【解析】
由不等式组解得a＞2．对于函数，令y=0，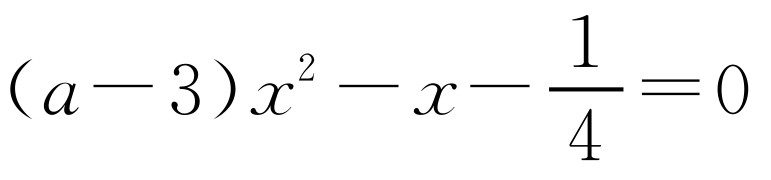
，当函数为二次函数即a-3≠0，a≠3时，
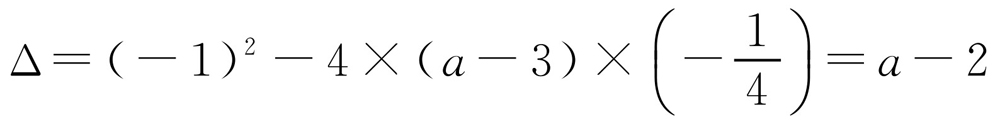，由于a＞2得到a-2＞0，故函数图像与x轴有2个交点；而当a=3时，函数为一次函数，此时图像与x轴有1个交点．综上，函数图像与x轴的交点个数为1或2个．
（☆☆☆）【巩固练习4】
对于函数f（x），若存在实数x0，使f（x0）=x0成立，则称x0为f（x）的不动点．已知函数f（x）=ax2+（b+1）x+b-1（a≠0），对于任意实数b，函数f（x）恒有两个相异的不动点，求a的取值范围．