【典型应用3】证明相关
(☆)【16.3.1】
设a+b>c>0,|a-b|<c,求证:二次方程a2x2+(b2+a2-c2)x+b2=0没有实数根.
【解析】
Δ=(b2+a2-c2)2-4a2·b2=[(a-b)2-c2][(a+b)2-c2]
由于a+b>c>0,|a-b|<c,可得(a-b)2-c2<0,(a+b)2-c2>0,故Δ<0,因此二次方程没有实数根.
(☆☆)【16.3.2】
已知a,b,c是△ABC的三边的长,方程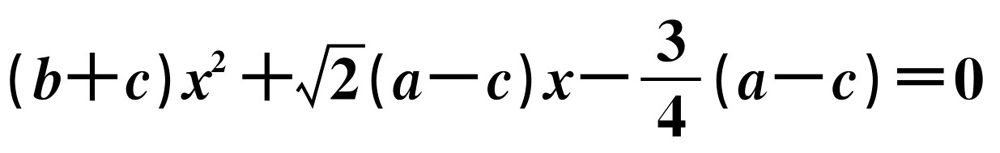 有两个相等的实数根,求证:△ABC是等腰三角形.
有两个相等的实数根,求证:△ABC是等腰三角形.
【解析】
由于方程有两个相等的实数根,
即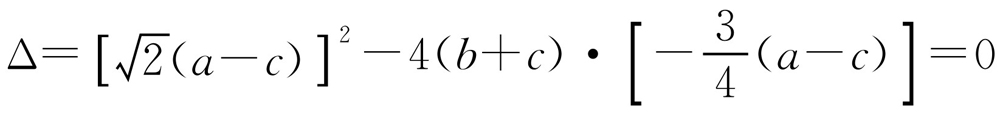 ,化简得(a-c)(2a+3b+c)=0.由a>0,b>0,c>0,有2a+3b+c>0,此时a-c=0,即a=c,△ABC是等腰三角形.
,化简得(a-c)(2a+3b+c)=0.由a>0,b>0,c>0,有2a+3b+c>0,此时a-c=0,即a=c,△ABC是等腰三角形.
(☆☆)【16.3.3】
已知实数a,b,c满足 ,求证b2≥4ac.
,求证b2≥4ac.
【解析】
分类讨论,当a=0时,无论b,c为何值,b2≥4ac=0总是成立的;当a≠0时,由a× ,也就是说方程ax2+bx+c=0有实根
,也就是说方程ax2+bx+c=0有实根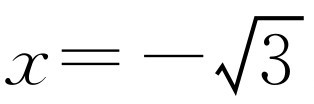 ,故Δ=b2-4ac≥0即b2≥4ac.综合分类情况即得证.
,故Δ=b2-4ac≥0即b2≥4ac.综合分类情况即得证.
(☆☆☆)【巩固练习3】
设实数a,b,c满足a+b+c=2,且对任何实数t,有-t2+2t≤ab+bc+ca≤9t2+18t+10.求证: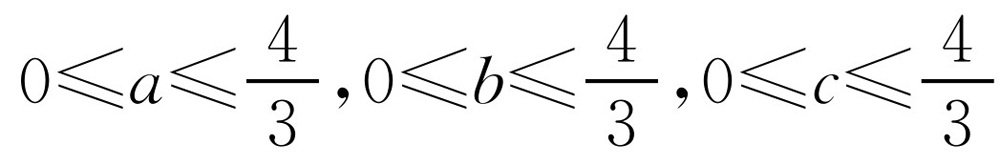 .
.