初中数学代数专题16判别式法【典型应用1】化简求值

【典型应用1】化简求值

（☆☆）【16.1.1】

已知关于x的方程x2+2（m+1）x+m2+5=0有两个不相等的实数根，化简：.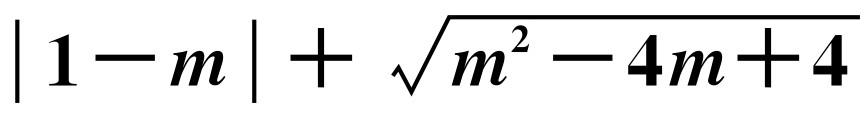

【解析】

由Δ=4（m2+2m+1）-4（m2+5）＞0，得m＞2，再化简得2m-3.

（☆☆）【16.1.2】

如果一直角三角形的三边为a，b，c，∠B=90°，试判断关于x的方程a（x2-1）-2cx+b（x2+1）=0的根的情况．

【解析】

由∠B=90°可得a2+c2=b2，化简原方程为（a+b）x2-2cx+b-a=0，Δ=4c2-4（b2-a2）=4c2-4c2=0，故方程有两个相等的实数根．

【备注】

勾股定理：如果直角三角形的两条直角边长分别为a和b，斜边长为c，那么a2+b2=c2.

（☆☆）【16.1.3】

已知x2-ax+3-b=0有两个不相等的实数根，x2+（6-a）x+6-b=0有两相等的实数根，x2+（4-a）x+5-b=0无实数根，求a，b的取值范围．

【解析】

x2-ax+3-b=0有两个不等的实数根，

Δ=a2-4（3-b）=a2+4b-12＞0　　　①，

x2+（6-a）x+6-b=0有两相等实根，

　　②，

x2+（4-a）x+5-b=0无实数根，

Δ=（4-a）2-4（5-b）=a2-8a+4b-4＜0　③，

②代入①得a＞2，②代入③得b＜4，由2＜a＜4，可得2＜b＜5．综上，2＜a＜4，2＜b＜5.

（☆☆☆）【16.1.4】

设x为实数，，试求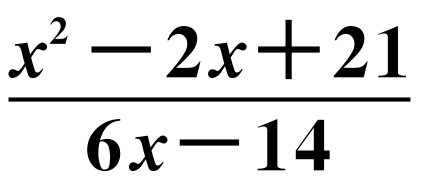的取值范围．

【解析】

令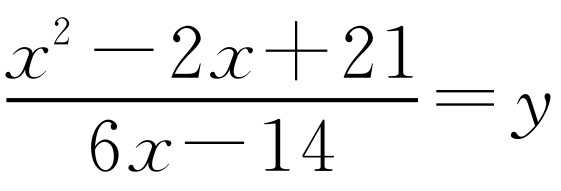，化简得x2-（2+6y）x+21+14y=0．由于x是实数，所以关于x的一元二次方程必有两个实根，即Δ=［-（2+6y）］2-4（21+14y）≥0，解出y的取值范围即得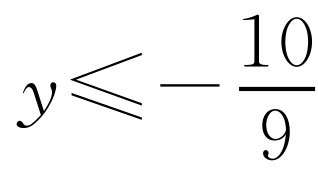或y≥2.

（☆☆☆）【16.1.5】

已知m，n为整数，方程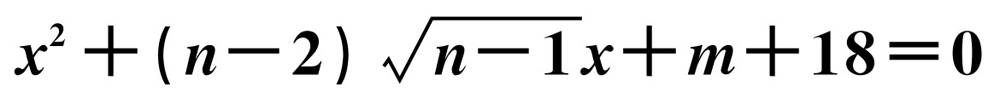有两个不相等的实数根，方程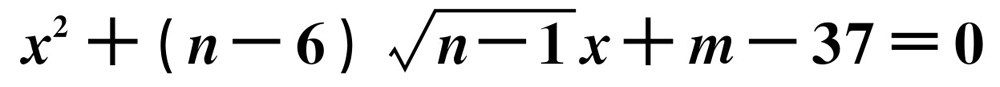有两个相等的实数根，求n的最小值并说明理由．

【解析】

有两个不相等的实数根，故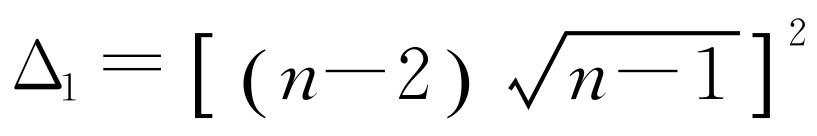，而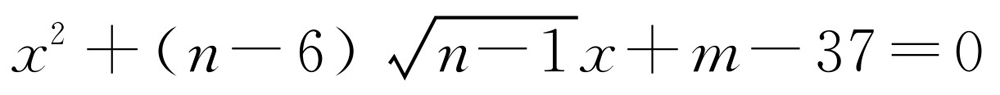有两个相等的实数根，故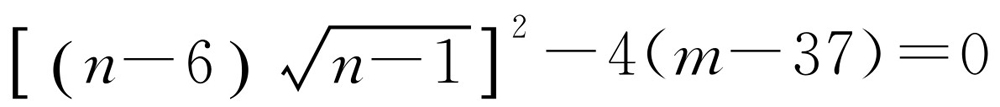，化简得4m=（n-6）2（n-1）+148，代入Δ1＞0中，化简得8n2-40n-188＞0，解得nmin=8.

（☆☆☆）【巩固练习1】