【典型应用2】代数式相关
（☆）【14.2.1】
已知a≠0，S1=2a，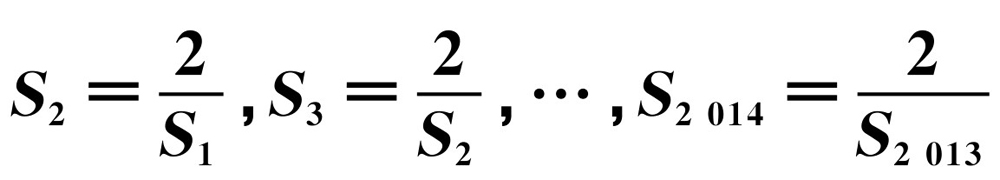
，则S2 014=________.（用含a的代数式表示）
【解析】
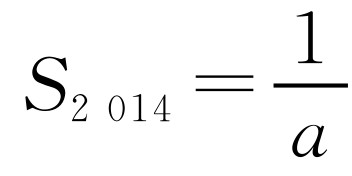.因为S1=2a，
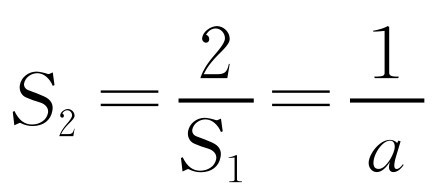，S3=2a，
，所以
.
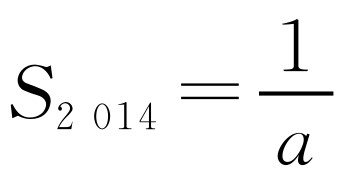（☆☆）【14.2.2】
观察下列等式：
12×231=132×21，
13×341=143×31，
23×352=253×32，
34×473=374×43，
62×286=682×26，
……
以上每个等式中两边数字是分别对称的，且每个等式中组成两位数与三位数的数字之间具有相同规律，我们称这类等式为“数字对称等式”.
（1）根据上述各式反映的规律填空，使式子成为“数字对称等式”.
①52×________=________×25；
②________×396=693×________.
（2）设这类等式左边两位数的十位数字为a，个位数字为b，且2≤a+b≤9，写出表示“数字对称等式”的一般规律的式子（含a，b）.
【解析】
通过归纳类比可知：等式左边，两位数所乘的数是这个两位数的个位数字变为百位数字，十位数字变为个位数字，两个数字的和放在十位．等式右边，三位数与左边的三位数字百位与个位数字交换，两位数与左边的两位数十位与个位数字交换后相乘．
（1）根据上述规律知：
①275，572.
②63，36.
（2）因为左边两位数的十位数字为a，个位数字为b，所以左边的两位数为10a+b，三位数是100b+10（a+b）+a，右边的两位数为10b+a，三位数是100a+10（a+b）+b，所以一般规律的式子为（10a+b）×［100b+10（a+b）+a］=［100a+10（a+b）+b］×（10b+a）.
（☆☆☆）【巩固练习2】
规律是数学研究的重要内容之一．初中数学中研究的规律主要有一些特定的规则、符号（数）及其运算规律、图形的数值特征和位置关系特征等方面．
请你解决以下与数的表示和运算相关的问题：
（1）写出奇数a用整数n表示的式子．
（2）写出有理数b用整数m和整数n表示的式子．
（3）函数的研究中，应关注y随x变化而变化的数值规律，下面对函数y=x2的某种数值变化规律进行初步研究：
由表看出，当x的取值从0开始每增加1个单位时，y的值依次增加1，3，5，…
请回答：
当x的取值从0开始每增加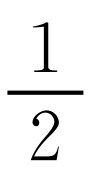
个单位时，y的值变化规律是什么？
当x的取值从0开始每增加
个单位时，y的值变化规律是什么？
