【典型应用1】数字相关
(☆)【14.1.1】
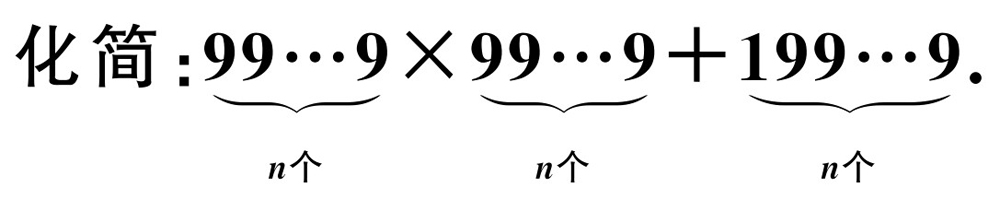
【解析】
102n.先考察n=1,2,3时的简单情形,然后作出猜想.
(☆☆)【14.1.2】
求1+2+22+23+…+22 012的值,可令S=1+2+22+23+…+22 012,则2S=2+22+23+…+22 013,所以2S-S=22 013-1,仿照以上推理,计算1+5+52+53+…+52 012的值,并猜想1+x+x2+…+xn的值.
【解析】
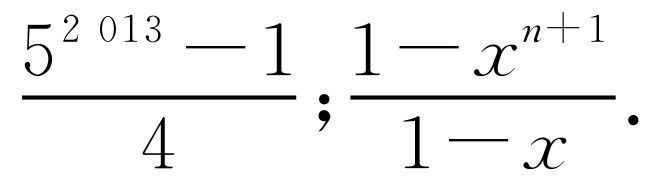
(☆☆☆)【14.1.3】
大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…,若m3分裂后,其中有一个奇数是2 013,则m的值为( ).
A.43
B.44
C.45
D.46
【解析】
C.根据归纳类比可知m3分裂后的第一个数是m(m-1)+1,共有m个奇数.
因为45×(45-1)+1=1 981,46×(46-1)+1=2 071,所以2 013是底数为45的数的立方分裂后的一个奇数,所以m=45.
(☆☆☆)【巩固练习1】
一串数排成一行,它们的规律是这样的:头两个数都是1,从第三个数开始,每一个数都是前两个数的和,也就是1,1,2,3,5,8,13,21,34,55,…,这串数的前100个数中(包括第100个数),有多少个偶数?