【典型应用】综合题
(☆☆☆)【10.1.1】
如图10-1所示,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A,B重合).OD⊥BC,OE⊥AC,垂足分别为D,E.
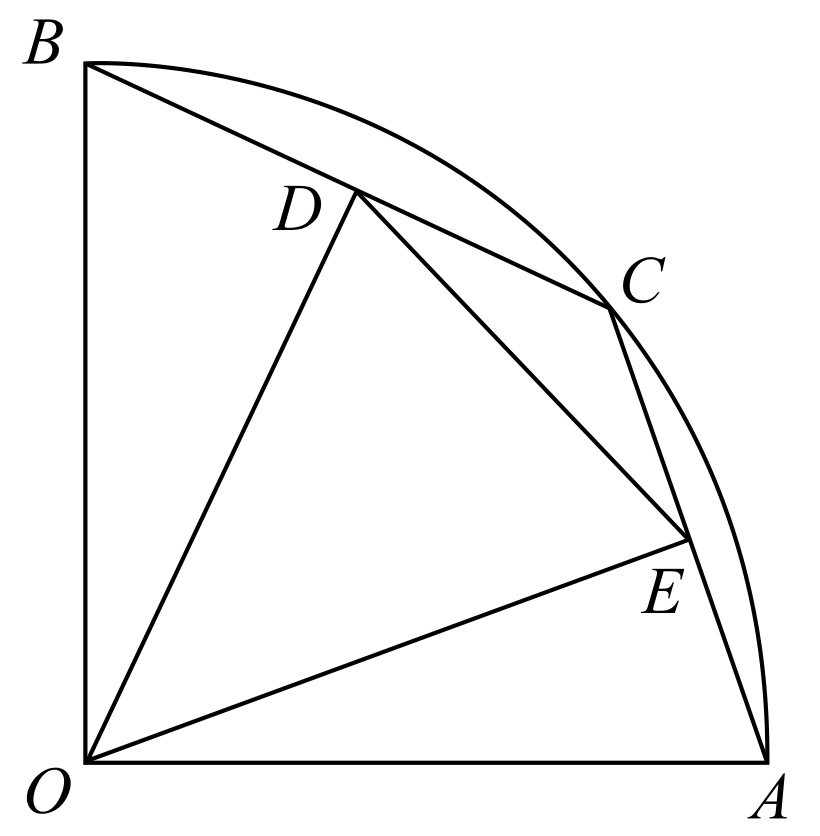
图10-1
(1)当BC=1时,求线段OD的长.
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.
(3)设BD=x,△DOE的面积为y,求y关于x的函数关系式,并写出它的定义域.
【解析】
由分析综合得:
(1)根据OD⊥BC可得出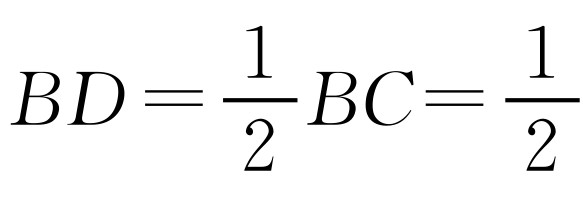 ,在Rt△BOD中利用勾股定理即可求出OD的长为
,在Rt△BOD中利用勾股定理即可求出OD的长为 .
.
(2)如图10-2所示,连接AB,由△AOB是等腰直角三角形可得出AB的长.再根据D和E是中点可得出 .
.

图10-2
(3)如图10-3所示,由BD=x,可知CD=x.由于∠1=∠2,∠3=∠4,所以∠2+∠3=45°.过D作DF⊥OE,连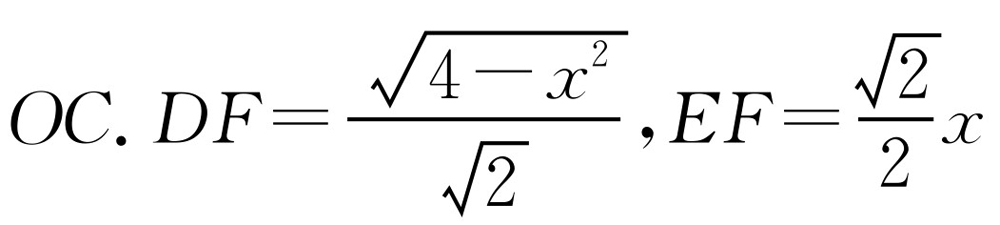 ,即可得出结论:
,即可得出结论:
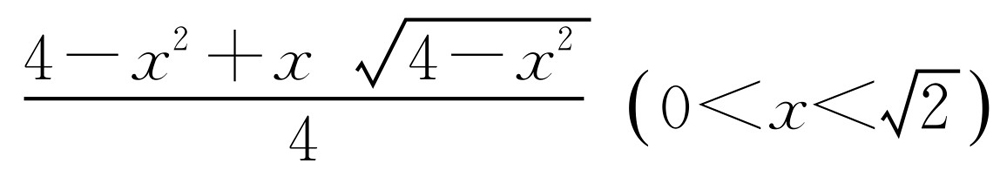 .
.
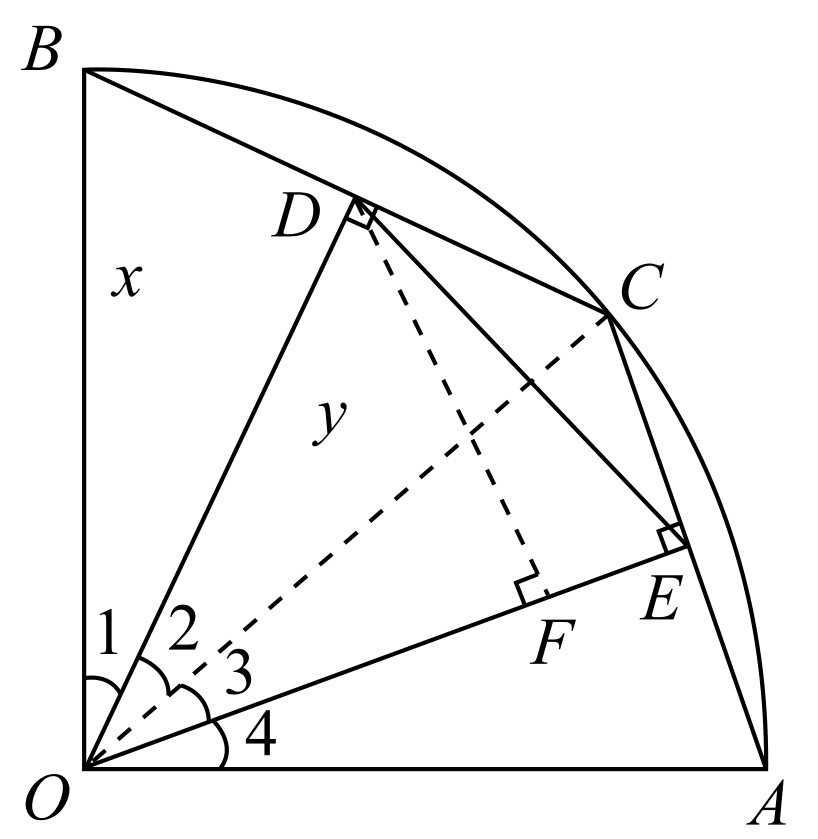
图10-3
(☆☆☆)【10.1.2】
如图10-4所示,已知抛物线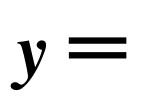
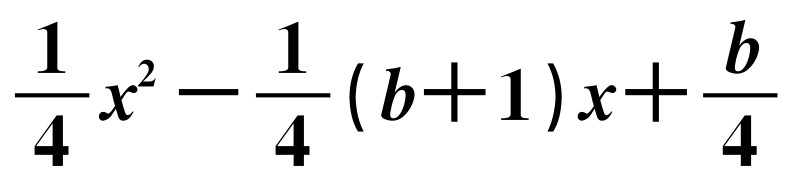 (b是实数且b>2)与x轴的正半轴分别交于点A,B(点A位于点B的左侧),与y轴的正半轴交于点C.
(b是实数且b>2)与x轴的正半轴分别交于点A,B(点A位于点B的左侧),与y轴的正半轴交于点C.
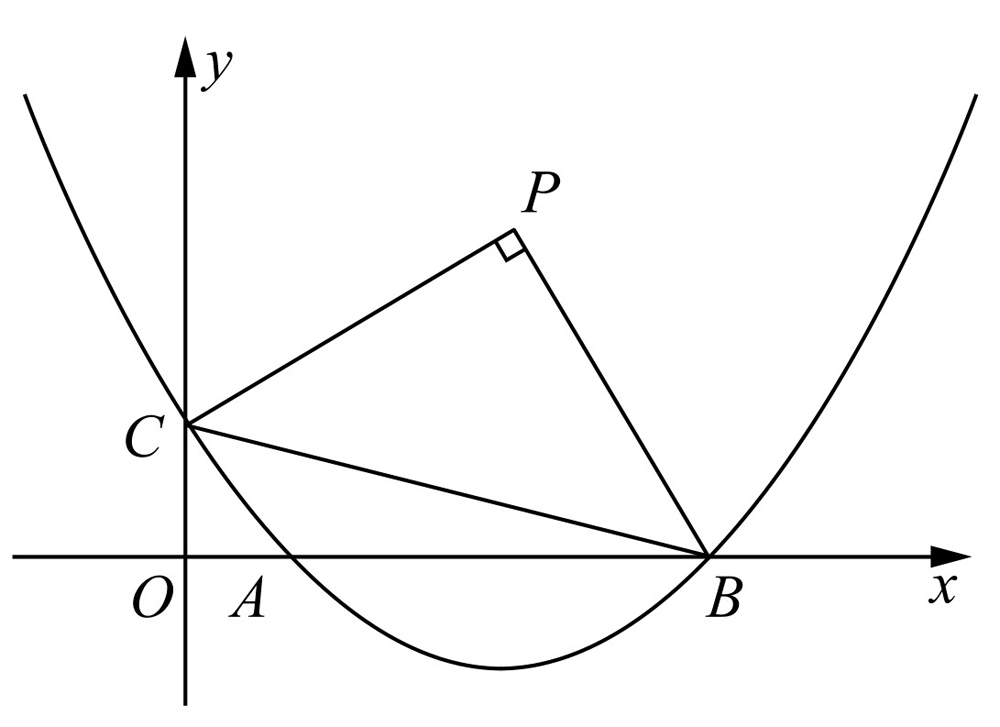
图10-4
(1)点B的坐标为________,点C的坐标为________(用含b的代数式表示).
(2)请你探索在第一象限内是否存在点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由.
(3)请你进一步探索在第一象限内是否存在点Q,使得△QCO,△QOA和△QAB中的任意两个三角形均相似(全等可作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由.
【解析】
(1)令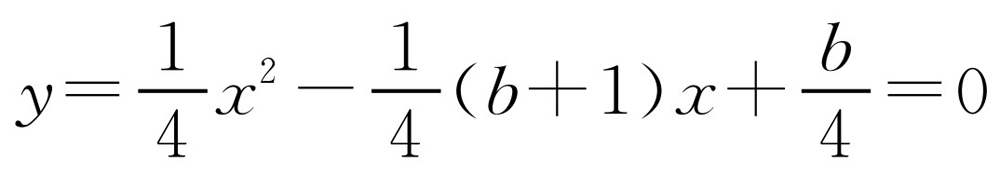 ,解关于x的一元二次方程即可求出A,B横坐标,令x=0,求出y的值即C的纵坐标,故得B(0,b),
,解关于x的一元二次方程即可求出A,B横坐标,令x=0,求出y的值即C的纵坐标,故得B(0,b),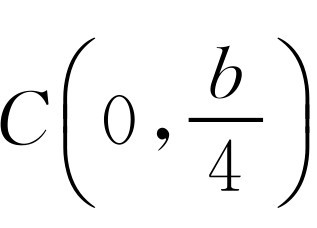 .
.
(2)如图10-5所示,过点P作PD⊥x轴,PE⊥y轴,垂足分别为D,E,那么△PDB≌△PEC.因此PD=PE.设点P的坐标为(x,x).如图10-6所示,连接OP.所以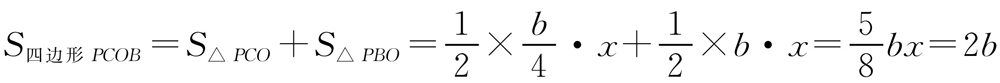 .解得
.解得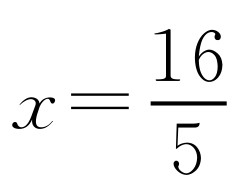 .所以存在点P,点P的坐标为
.所以存在点P,点P的坐标为 .
.
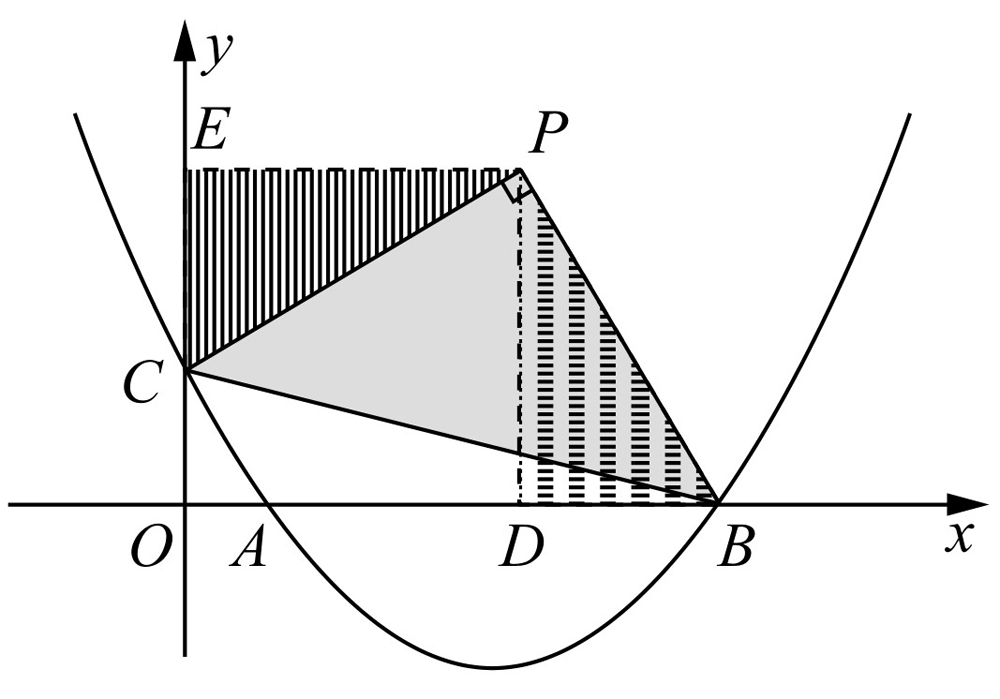
图10-5

图10-6
(3)由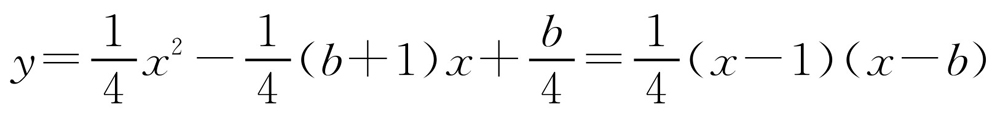 ,得A(1,0),OA=1.
,得A(1,0),OA=1.
①如图10-7所示,以OA,OC为邻边构造矩形OAQC,那么△OQC≌△QOA.当 ,即QA2=BA·OA时,△BQA∽△QOA.所以
,即QA2=BA·OA时,△BQA∽△QOA.所以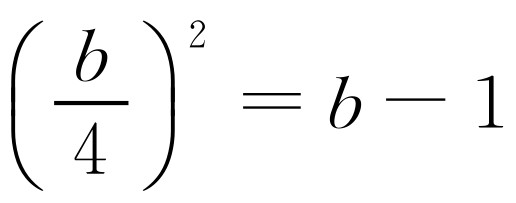 .解得
.解得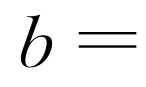
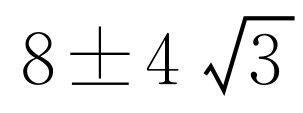 .所以符合题意的点Q为(
.所以符合题意的点Q为( ).
).
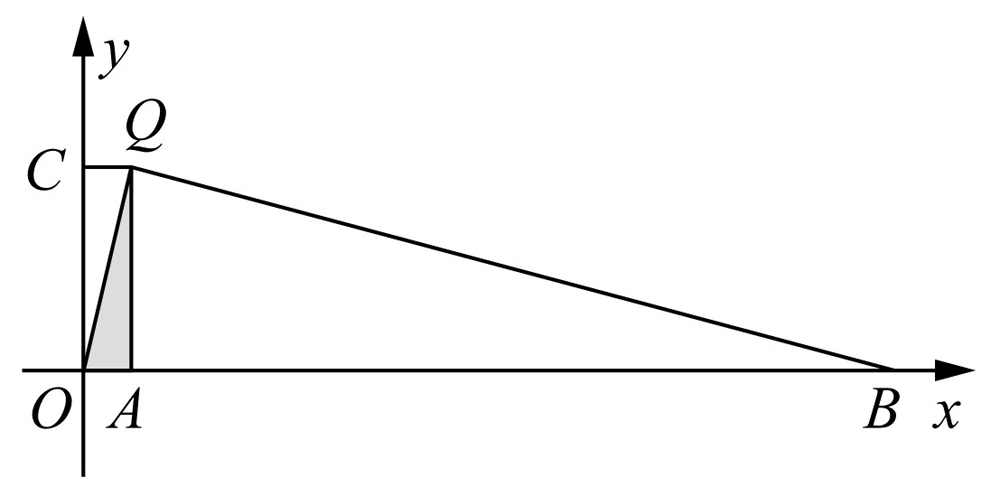
图10-7
②如图10-8所示,以OC为直径的圆与直线x=1交于点Q,那么∠OQC=90°.因此△OCQ∽△QOA.当 时,△BQA∽△QOA.此时∠OQB=90°.所以C,Q,B三点共线.因此
时,△BQA∽△QOA.此时∠OQB=90°.所以C,Q,B三点共线.因此 ,即
,即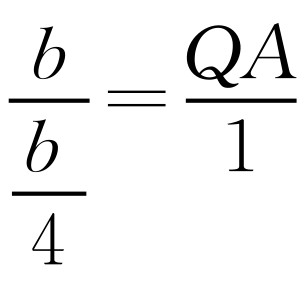 .解得QA=4.此时点Q为(1,4).
.解得QA=4.此时点Q为(1,4).

图10-8
综上,存在点Q,点Q坐标为 或(1,4).
或(1,4).
(☆☆☆)【巩固练习1】
已知抛物线C1的函数解析式为y=ax2+bx-3a(b<0),若抛物线C1经过点(0,-3),方程ax2+bx-3a=0的两根为x1,x2,且|x1-x2|=4.
(1)求抛物线C1的顶点坐标.
(2)已知实数x>0,请证明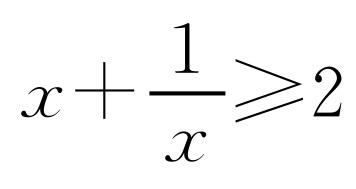 ,并说明x为何值时才会有
,并说明x为何值时才会有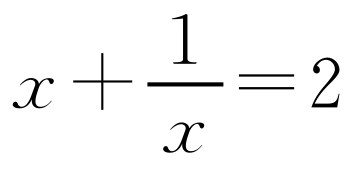 .
.
(3)若抛物线先向上平移4个单位,再向左平移1个单位后得到抛物线C2,设A(m,y1),B(n,y2)是C2上的两个不同点,且满足∠AOB=90°,m>0,n<0.请你用含有m的表达式表示出△AOB的面积S,并求出S的最小值及S取最小值时一次函数OA的函数解析式。
(参考公式:在平面直角坐标系中,若P(x1,y1),Q(x2,y2),则P,Q两点间的距离为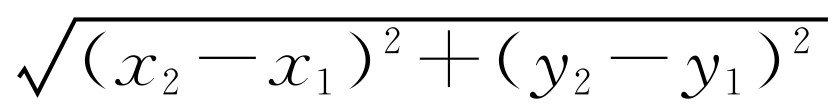 .)
.)