【典型应用2】凑变相关
（☆☆）【8.2.1】
目前某单位女职工和男职工的人数之比为1:30，如果女职工的人数增加5人，男职工的人数增加50人，则两者之比变为1:25，求目前女职工的人数．
【解析】
标准量的比例关系为1:30，但现在女职工和男职工增加人数之比并不是1:30，这时就需要“凑变”，那么我们可以让男职工多增加100人，这样就是1:30，其结果也就是1:30，而实际情况是1:25，减少了30-25=5个标准量就对应这100个男职工了，所以每个标准量就是20人．所以女职工是在增加5人之后构成的1个标准量，即原来女职工人数是20-5=15（人）.
（☆☆☆）【8.2.2】
客车与货车分别从A，B两地同时相对开出，已知客车与货车的速度比为4:5，两车在途中相遇后，继续往前行驶，此时货车提速20%，客车的速度不变．再过4小时后，货车到达A地，而客车离B地还有112千米，则A，B两地的距离为多少？
【解析】
如图8-1所示，设两车在点C相遇，那么AC:CB=4:5，当货车提速20%后，客车与货车的速度比变为4:（5×1.2）=2:3，假设当货车到达A时，客车到达D处，即AC:CD=3:2，我们可把AC的路程调整到3与4的最小公倍数12个标准量，则AC:CB=4:5=12:15，全程为12+15=27，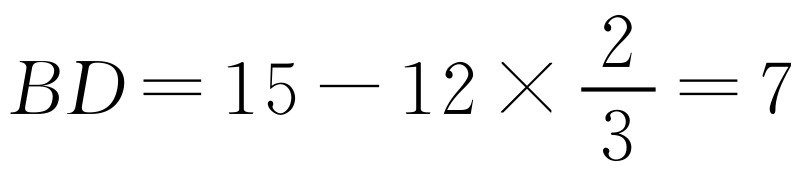
，所以AB两地的距离为112÷7×27=432（千米）.
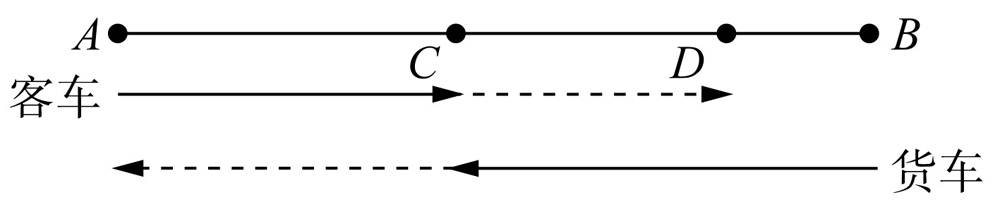
图8-1
（☆☆☆）【巩固练习2】
有黑白棋子一堆，黑子的个数是白子的2倍，如果从这堆棋子中每次同时取出黑子4枚、白子3枚．几次以后，白子余1枚，黑子余18枚？