初中数学代数专题8比例法【典型应用1】标准量相关

【典型应用1】标准量相关

（☆☆）【8.1.1】

一项机械加工作业，用4台A型车床，5天可以完成，用4台A型车床和2台B型车床，3天可以完成，用3台B型车床和9台C型车床，2天可以完成，若A型、B型、C型车床各一台一起工作4天后，只余下B型车床继续工作，再用几天就可以完成这项作业？

【解析】

假设总工作量为1，则每台A型车床每天的工作效率为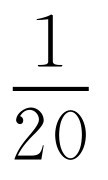，每台B型车床每天的工作效率为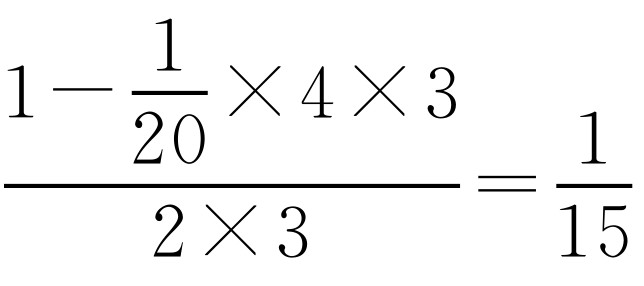，每台C型车床每天的工作效率为.三台机床一起工作4天后，还需要的时间为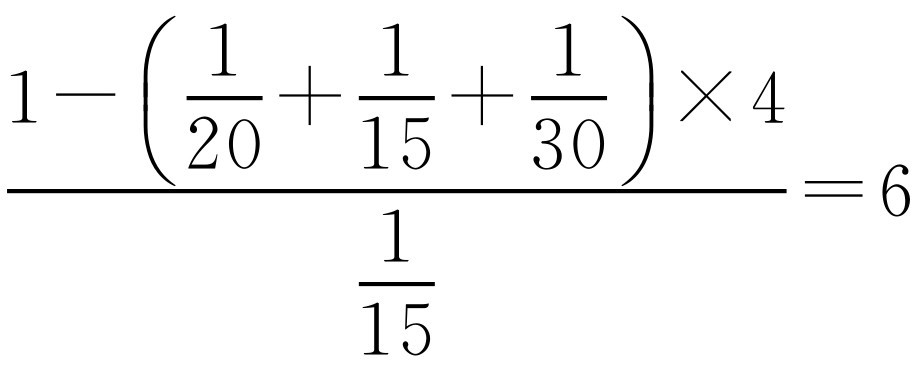（天）.

（☆☆☆）【8.1.2】

甲、乙两人从两地同时出发相向匀速而行，5小时后在点M相遇．若条件不变，甲每小时提速4千米，乙速度不变，则距点M6千米相遇；若甲速度不变，乙每小时提速4千米，则相距点M12千米，求甲、乙两人的速度之比．

【解析】

如果按照原来相遇的时间5小时走，那么甲提速4千米，则偏离第一次相遇的点M有4×5=20千米，而乙在M上，也就是说相同的时间内，甲、乙从相遇到乙走到点M，乙走了6千米，而甲走了20-6=14（千米）．因此甲、乙的速度比是14:6=7:3，同理如果乙提速，跟5小时的时候对比，甲走12千米，则乙走了20-12=8（千米）．甲、乙速度之比为12:8=3:2，又因为7:3=28:12，3:2=24:16，均相差4个标准量，因此甲、乙的速度之比为24:12=2:1.

（☆☆）【巩固练习1】