初中数学代数专题7反证法【典型应用3】证明相关

【典型应用3】证明相关

（☆☆）【7.3.1】

若n是正整数，证明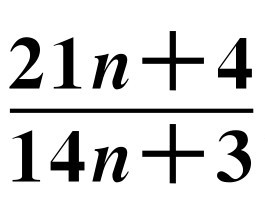：是最简分数．

【解析】

设不是最简分数，则设21n+4与14n+3的公约数为k（k≠1，k为正整数），即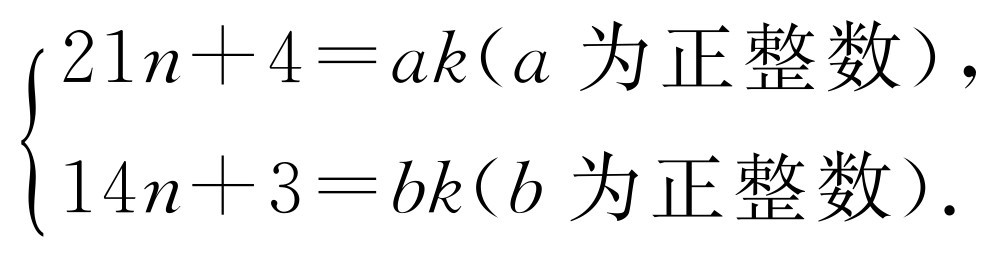则即，3bk-2ak=1，（3b-2a）k=1．因为a，b，k均为正整数，所以与假设k≠1矛盾，所以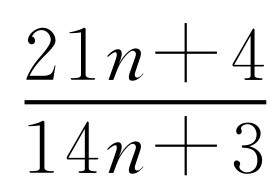是最简分数．

（☆☆）【7.3.2】

求证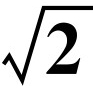：是无理数．

【解析】

假设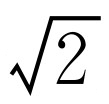是有理数，则存在互质的整数m，n，使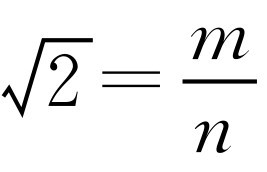，所以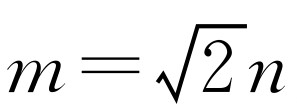，即m2=2n2，所以m2是偶数，m也为偶数．再设m=2k（k为正整数），所以4k2=m2=2n2，即n=2k2，所以n也为偶数，这与m，n互质这一条件矛盾，所以假设不成立，从而知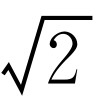是无理数．

（☆☆）【巩固练习3】