【典型应用2】“至少”“至多”型命题
（☆☆）【7.2.1】
设a，b，c是不全相等的实数，若x=a2-bc，y=b2-ac，z=c2-ab，求证：x，y，z中至少有一个大于零．
【解析】
假设x，y，z都不大于零．
则x+y+z=a2-bc+b2-ac+c2-ab≤0.
而2（x+y+z）=2（a2-bc+b2-ac+c2-ab）=（a-b）2+（b-c）2+（a-c）2≥0.
所以只能x+y+z=0，即（a-b）2+（b-c）2+（a-c）2=0.
此时a=b=c，这与已知条件a，b，c是不全相等的实数矛盾，所以x，y，z中至少有一个大于零．
（☆☆）【7.2.2】
设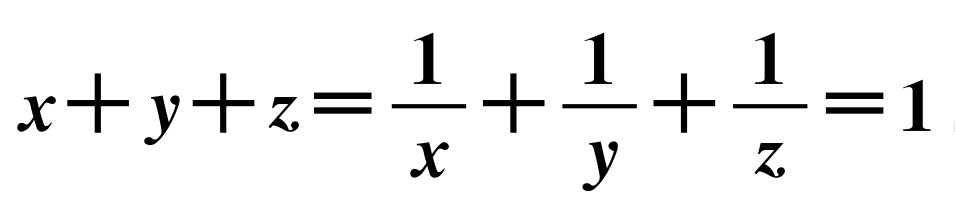
，求证：x，y，z中至少有一个等于1.
【解析】
假设x，y，z中都不等于1，则（x-1）（y-1）（z-1）≠0.
即xyz-xy-xz+x-yz+y+z-1≠0，又因为x+y+z=1，所以xyz-xy-xz-yz≠0.
两边同除xyz并整理得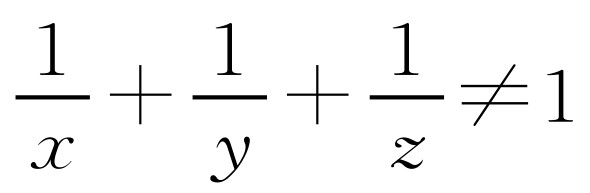
，与已知条件
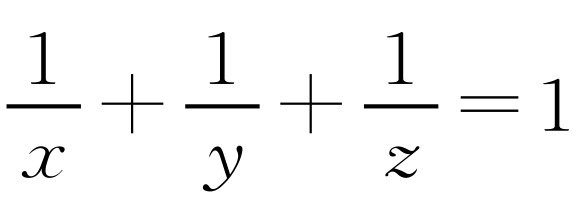矛盾，所以x，y，z中至少有一个等于1.
（☆☆☆）【巩固练习2】
已知：f（x）=x2+px+q，求证：|f（1）|，|f（2）|，|f（3）|中至少有一个不小于
.