初中数学代数专题6公式法【典型应用4】证明相关

【典型应用4】证明相关

（☆☆☆）【6.4.1】

已知a，b，c都是自然数，a+b+c=1，求证：.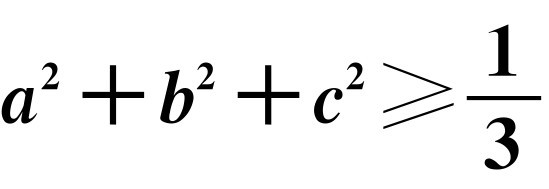

【解析】

由于当时，符合条件且能使结论中的等号成立，此时a2，b2，c2的值都是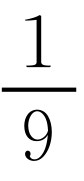.同时考虑到要将次数降到一次才好利用已知条件，所以为它们都配上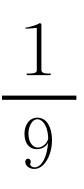，由此利用基本不等式a2+b2≥2ab，可得．三式相加得，故得证．

【备注】

基本不等式：a2+b2≥2ab（当且仅当a=b时等号成立）.

（☆☆☆）【6.4.2】

设|a|+|b|＜1，且关于x的一元二次方程x2+ax+b=0有实根．求证：关于x的一元二次方程x2+ax+b=0的两根的绝对值均小于1.

【解析】

设关于x的一元二次方程的两个实根为x1，x2（|x1|＞|x2|）．由韦达定理，x1+x2=-a，x1x2=b．故|a|+|b|=|-a|+|b|=|x1+x2|+|x1x2|＜1，由于|x1|-|x2|≤|x1+x2|，|x1x2|=|x1|·|x2|，故|x1|-|x2|+|x1|·|x2|≤|x1+x2|+|x1x2|＜1，（|x1|-1）（|x2|+1）＜0．由于|x2|+1＞0，故|x1|-1＜0，|x1|＜1，|x2|＜|x1|＜1．故得证．

【备注】

|x|-|y|≤|x±y|≤|x|+|y|（当且仅当x=y等号成立）.

（☆☆）【巩固练习4】

【备注】

特别地，当a+b+c=0时，a3+b3+c3=3abc.