初中数学代数专题5十字相乘法【典型应用2】化简求值

【典型应用2】化简求值

（☆☆）【5.2.1】

已知x4-10x3+35x2-50x+24＞0，求x的取值．

【解析】

x4-10x3+35x2-50x+24＞0，用十字相乘法可变形为（x-1）（x-2）（x-3）×（x-4）＞0．所以，x＜1或2＜x＜3或x＞4.

（☆☆）【5.2.2】

证明：若4x-y是7的倍数，其中x，y都是整数，则8x2+10xy-3y2是49的倍数．

【解析】

因为4x-y是7的倍数，设4x-y=7m（m是整数），则y=4x-7m，用十字相乘法可得8x2+10xy-3y2=（2x+3y）（4x-y），将y代入后8x2+10xy-3y2=（2x+12x-21m）（4x-4x+7m）=49m（2x-3m），由题知，m是整数，则m（2x-3m）也是整数，从而8x2+10xy-3y2是49的倍数．

（☆☆☆）【5.2.3】

解关于x的方程：a2（x2-x+1）-a（x2-1）=（a2-1）x.

【解析】

原式可化为（a2-a）x2+（1-2a2）x+a2+a=0，由十字相乘法可得

［（a-1）x-a］［ax-（a+1）］=0，

a≠0且a≠1时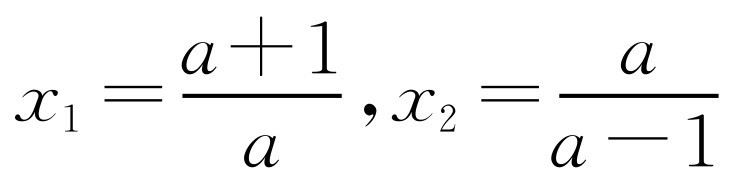，.当a=0时，x=0；当a=1时，x=2.

（☆☆☆）【5.2.4】

正数m，n满足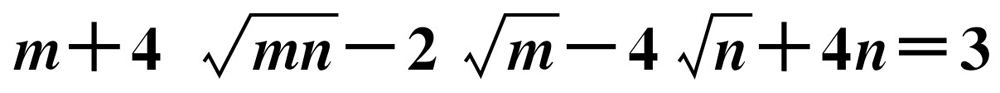，则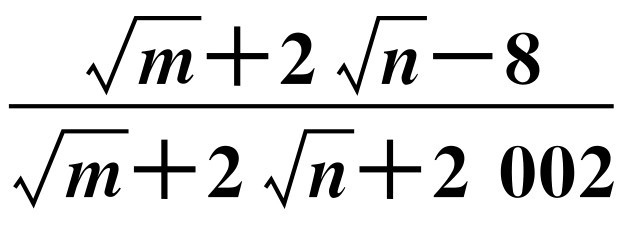的值为多少．

【解析】

令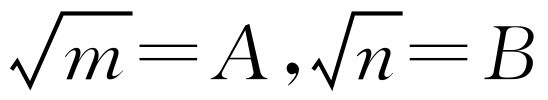，则A2+4AB-2A-4B+4B2-3=0.

整理得（A+2B）2-2（A+2B）-3=0.

（A+2B-3）（A+2B+1）=0.

故A+2B=3，A+2B+1=0（舍）.

（☆☆）【巩固练习2】