初中数学代数专题5十字相乘法【典型应用1】因式分解

【典型应用1】因式分解

（☆☆）【5.1.1】

分解因式14x2-67xy+18y2.

【解析】

把14x2-67xy+18y2看成一个关于x的二次三项式，y看成常数．

14x2-67xy+18y2

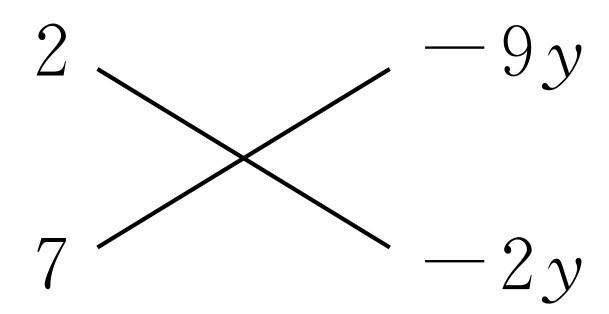
则14x2-67xy+18y2=（2x-9y）（7x-2y）.

（☆☆☆）【5.1.2】

分解因式2x2-7xy-22y2-5x+35y-3.

【解析】

按x降幂排列，并把y当作常数，整理得2x2-（5+7y）x-（22y2-35y+3）.

2x2-（5+7y）x-（22y2-35y+3）

2x2-7xy-22y2-5x+35y-3=［x+（2y-3）］［2x+（-11y+1）］=（x+2y-3）（2x-11y+1）.

【备注】

形如ax2+bxy+cy2+dx+ey+f的因式分解步骤：

（1）用十字相乘法分解ax2+bxy+cy2（注意把y看成常数），有两列．

（2）把常数项f分解为两个因式写在第三列，其中第二列与第三列构成的十字相乘图交叉相乘再相加的和等于原式中的ey，第一列与第三列构成的十字相乘图交叉相乘再相加的和等于原式中的dx.

2x2-7xy-22y2-5x+35y-3.

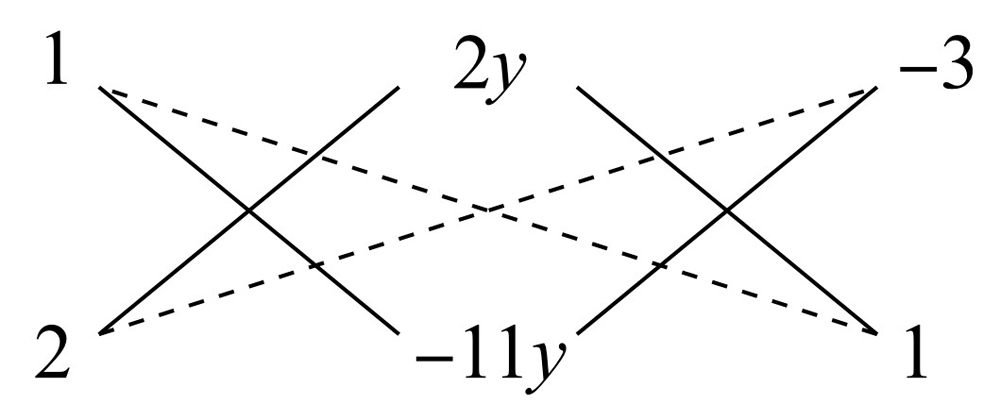
1×（-11y）+2×2y=-7y，2y×1+（-3）×（-11y）=35y，1×1+（-3）×2=-5（也可用待定系数法，略）

（☆☆）【巩固练习1】