【典型应用3】综合应用
(☆☆☆)【4.3.1】
已知关于x的一元二次方程x2-2(k+1)x+k2-2k-3=0有两个不相等的实数根.
(1)求k的取值范围.
(2)当k取最小的整数时,求抛物线y=x2-2(k+1)x+k2-2k-3的顶点坐标以及它与x轴的交点坐标.
(3)将(2)中求得的抛物线在x轴下方的部分沿x轴翻折到x轴上方,图像的其余部分不变,得到一个新图像.请你画出这个新图像,并求出新图像与直线y=x+m有三个不同公共点时m的值.
【解析】
(1)由题意,得Δ=4(k+1)2-4(k2-2k-3)=16k+16>0,所以k>-1.所以k的取值范围为k>-1.
(2)k>-1,且k取最小的整数,所以k=0.所以y=x2-2x-3=(x-1)2-4,则抛物线的顶点坐标为(1,-4),因为y=x2-2x-3的图像与x轴相交,所以0=x2-2x-3,所以解得:x=-1或3,所以抛物线与x轴相交于A(-1,0),B(3,0);
(3)翻折后所得新图像如图4-11所示.平移直线y=x+m知:直线位于l1和l2时,它与新图像有三个不同的公共点.①当直线位于l1时,此时l1过点A(-1,0),所以0=-1+m,即m=1.②当直线位于l2时,此时l2与函数y=-x2+2x+3的图像有一个公共点,所以方程x+m=-x2+2x+3,即x2-x+m-3=0有两个相等实根,所以Δ=1-4(m-3)=0,即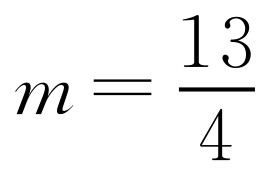 .当
.当 时,
时,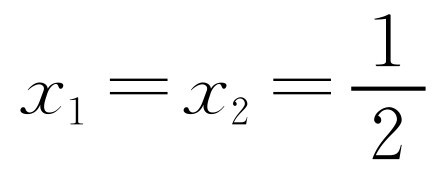 ,满足-1≤x≤3.由①②知m=1或
,满足-1≤x≤3.由①②知m=1或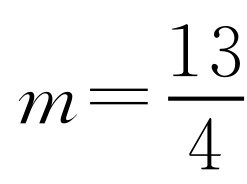 .
.
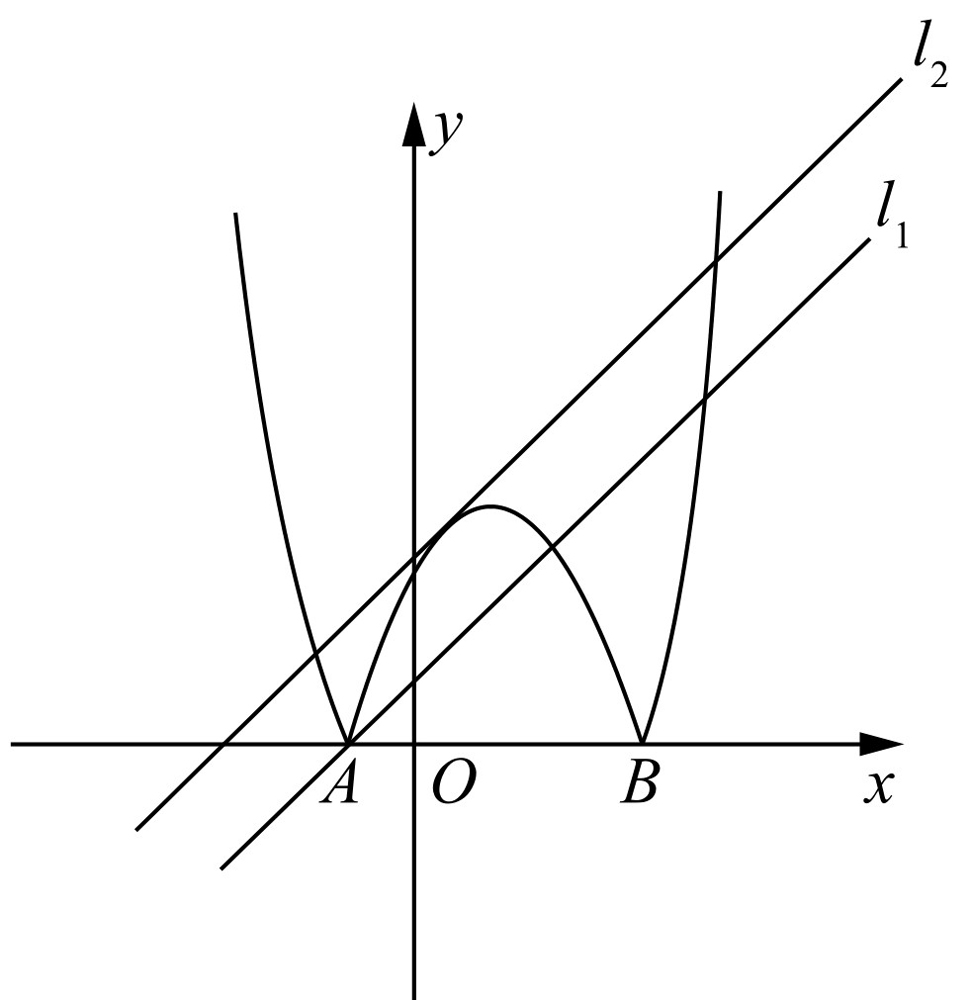
图4-11
(☆☆☆)【4.3.2】
如图4-12所示,抛物线C1:y=-x2+4x-2与x轴交于A,B,直线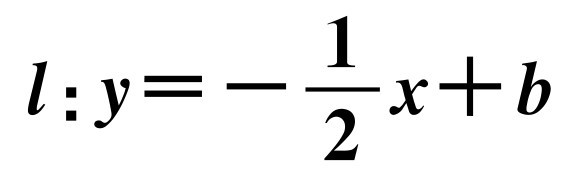 分别交x轴、y轴于点S和点C,抛物线C1的顶点E在直线l上.
分别交x轴、y轴于点S和点C,抛物线C1的顶点E在直线l上.
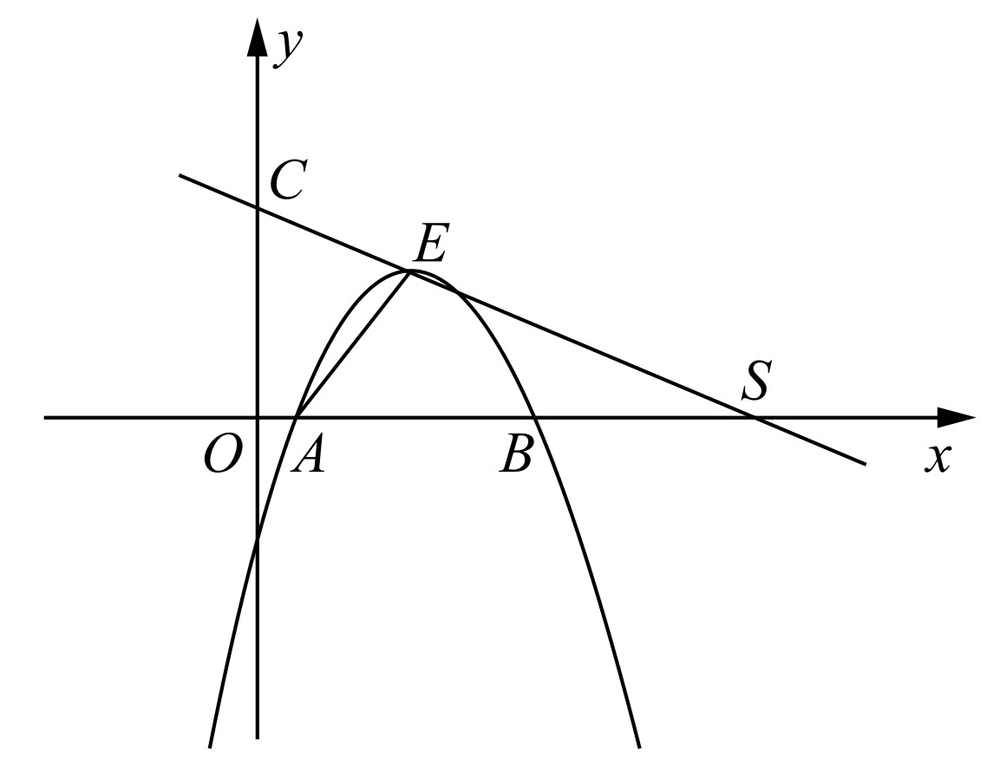
图4-12
(1)求直线l的解析式.
(2)如图4-13所示,将抛物线C1沿射线ES的方向平移得到抛物线C2,抛物线C2的顶点F在直线l上,并交x轴于M,N两点,且
 ,求抛物线C1平移的距离.
,求抛物线C1平移的距离.

图4-13
(3)将抛物线C2沿水平方向平移得到抛物线C3,抛物线C3与x轴交于P,G两点(点P在点G的左侧),使得△PEF为直角三角形,求抛物线C3的解析式.
【解析】
(1)因为抛物线C1:y=-x2+4x-2=-(x-2)2+2,则顶点E(2,2),代入直线l的解析式后,得b=3.直线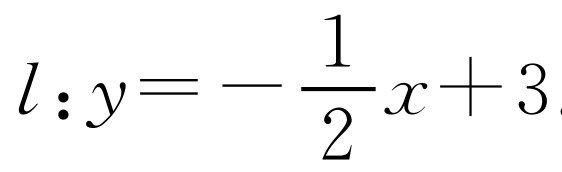 .
.
(2)因为顶点F在直线l上,设顶点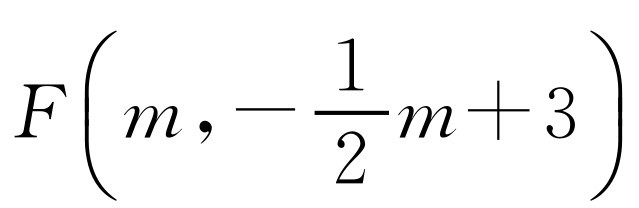 ,抛物线C2可表示为
,抛物线C2可表示为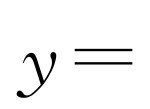
 .所以
.所以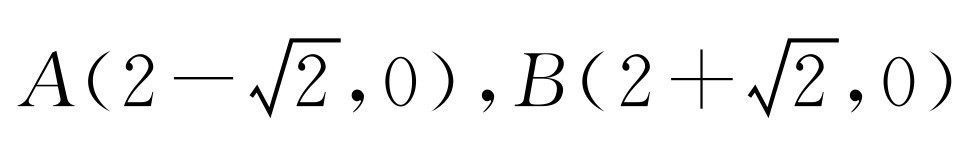 ,E(2,2),
,E(2,2), ;因为
;因为 ,所以tan∠FNM=1,∠FNM=45°,所以
,所以tan∠FNM=1,∠FNM=45°,所以
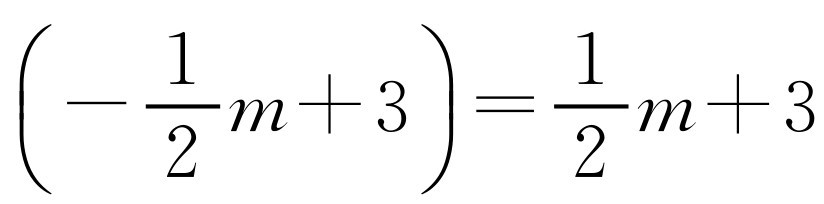 ,即
,即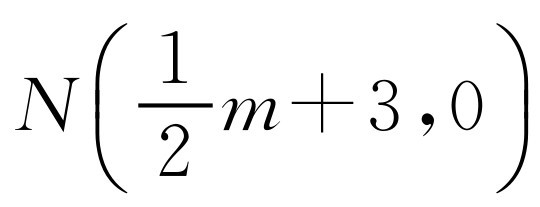 .代入
.代入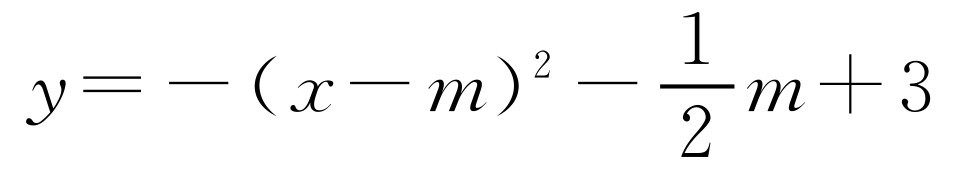 中,得m=4,即F(4,1);所以
中,得m=4,即F(4,1);所以 ,即抛物线C1平移的距离
,即抛物线C1平移的距离 .
.
(3)由(2)知C2:y=-(x-4)2+1,所以M(3,0),N(5,0).因为PG=MN=2,设P(p,0),则Q(p+2,0),抛物线C3顶点(p+1,1),抛物线C3:y=-(x-p-1)2+1.因为E(2,2),F(4,1),所以PE2=(p-2)2+22=p2-4p+8;PF2=(p-4)2+12=p2-8p+17,EF2=5.
①当∠PEF=90°时,p2-4p+8+5=p2-8p+17,所以p=1,此时C3为y=-(x-2)2+1;
②当∠PFE=90°时,p2-8p+17+5=p2-4p+8,所以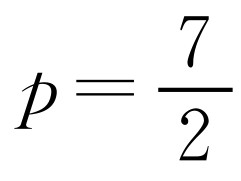 ,此时C3为y=
,此时C3为y=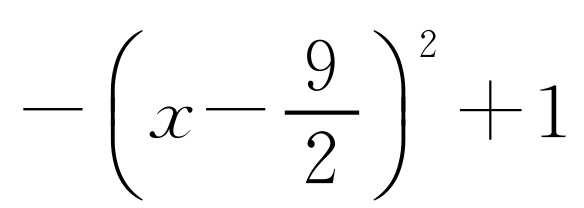 ;
;
③当∠EPF=90°时,p2-8p+17+p2-4p+8=5,即p2-6p+10=0,Δ<0,此时C3不存在;
故抛物线C3的解析式为y=-(x-2)2+1或 .
.
(☆☆☆)【4.3.3】
如图4-14所示,抛物线y=ax2+bx+c与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,且当x=0和x=2时,y的值相等.直线y=3x-7与这条抛物线相交于两点,其中一点的横坐标是4,另一点是这条抛物线的顶点M.
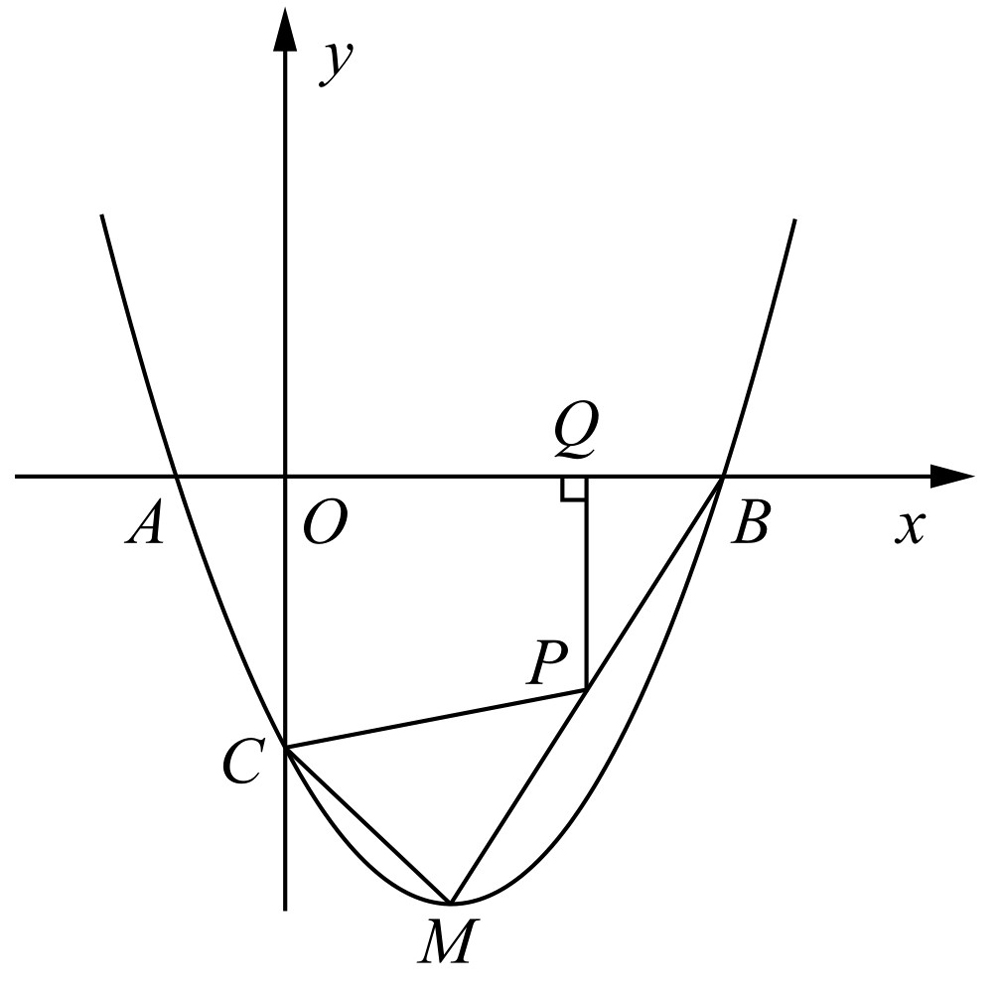
图4-14
(1)求这条抛物线的解析式.
(2)P为线段BM上一点,过点P向x轴引垂线,垂足为Q.若点P在线段BM上运动(点P不与点B,M重合),设OQ的长为t,四边形PQAC的面积为S.求S与t之间的函数关系式及自变量t的取值范围.
(3)在线段BM上是否存在点N,使△NMC为等腰三角形?若存在,请求出点N的坐标;若不存在,请说明理由.
【解析】
(1)由题意可知,抛物线的对称轴为x=1.
当x=1时,y=3x-7=-4,因此抛物线的顶点M的坐标为(1,-4).
当x=4时,y=3x-7=5,因此直线y=3x-7与抛物线的另一交点为(4,5).
设抛物线的解析式为y=a(x-1)2-4,则有a(4-1)2-4=5,a=1.故抛物线的解析式为y=x2-2x-3.
(2)根据(1)的抛物线可知:A(-1,0),B(3,0),C(0,-3),
易知直线BM的解析式为y=2x-6,
当x=t时,y=2t-6,因此PQ=6-2t,
故 ,
,
即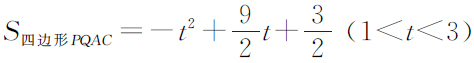 .
.
(3)假设存在这样的点N,使△NMC为等腰三角形.
因为点N在BM上,不妨设点N坐标为(m,2m-6),
则CM2=2,CN2=m2+[3-(6-2m)]2,或CN2=m2+[(6-2m)-3]2.
MN2=(m-1)2+[4-(6-2m)]2.
△NMC为等腰三角形,有以下三种可能:
①若CN=CM,则m2+[(6-2m)-3]2=2,所以 ,m2=1(舍去).所以
,m2=1(舍去).所以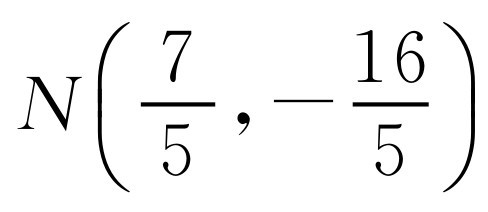 .
.
②若CM=MN,则2=(m-1)2+[4-(6-2m)]2.所以 .因为1<m<3,所以
.因为1<m<3,所以 舍去.所以
舍去.所以 .
.
③若CN=NM,则m2+[3-(6-2m)]2=(m-1)2+[4-(6-2m)]2.解得m=2.所以N(2,-2).故假设成立.
综上所述,存在这样的点N,使△NMC为等腰三角形,且点N的坐标分别为
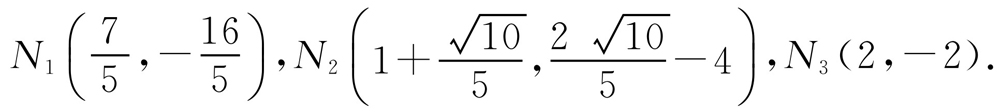
(☆☆☆)【巩固练习3】
如图4-15所示,在梯形ABCD中,AD∥BC,AB=AD=DC=2cm,BC=4cm,在等腰△PQR中,∠QPR=120°,底边QR=6cm,点B,C,Q,R在同一直线l上,且C,Q两点重合.如果等腰△PQR以1cm/秒的速度沿直线l以箭头所示方向匀速运动,t秒时梯形ABCD与等腰△PQR重合部分的面积记为S平方厘米.

图4-15
(1)当t=4时,求S的值.
(2)当4≤t≤10,求S与t的函数关系式,并求出S的最大值.