【典型应用2】几何相关
（☆☆）【4.2.1】
如图4-4所示，正方形ABCD的边长为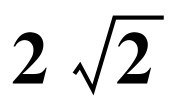
，过点A作AE⊥AC，AE=1，连接BE，求tan E的值．
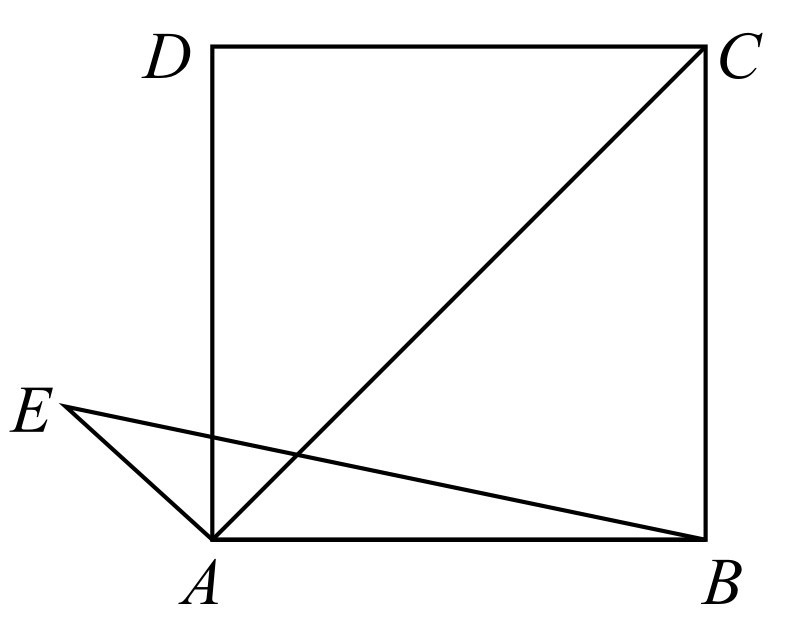
图4-4
【解析】
如图4-5所示，延长CA使AF=AE，连接BF，过点B作BG⊥AC，垂足为G，易证△BAF≌△BAE，得出∠E=∠F，在Rt△BGF中，求出tan F，进而求出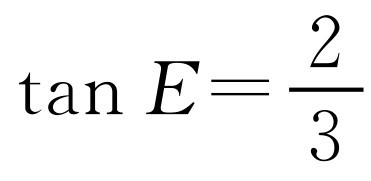
.
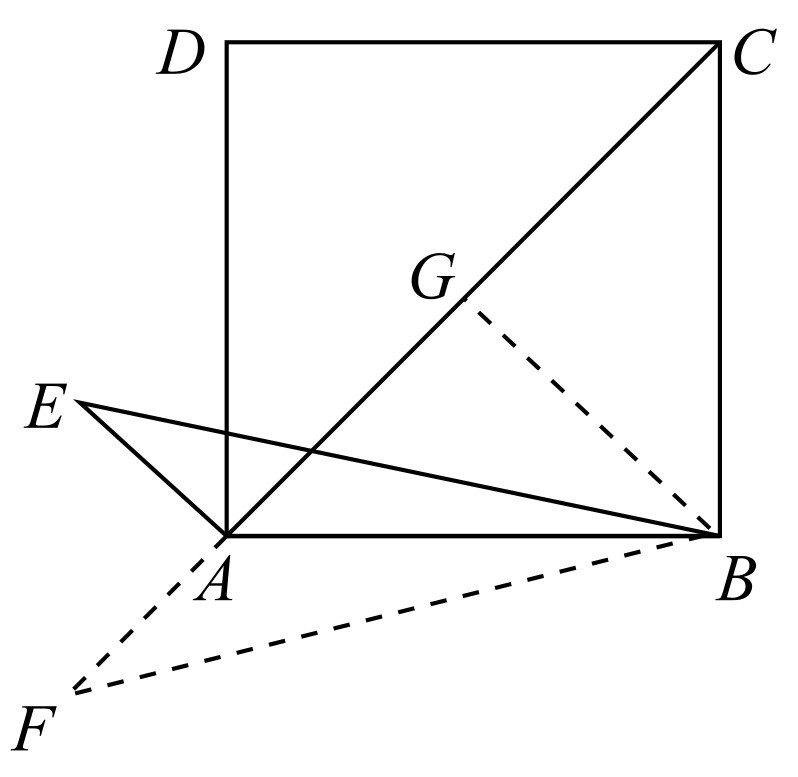
图4-5
（☆☆）【4.2.2】
如图4-6所示，∠C=∠D=90°，EF⊥AB，点F为垂足．求证：AB2=AE·AD+BE·BC.
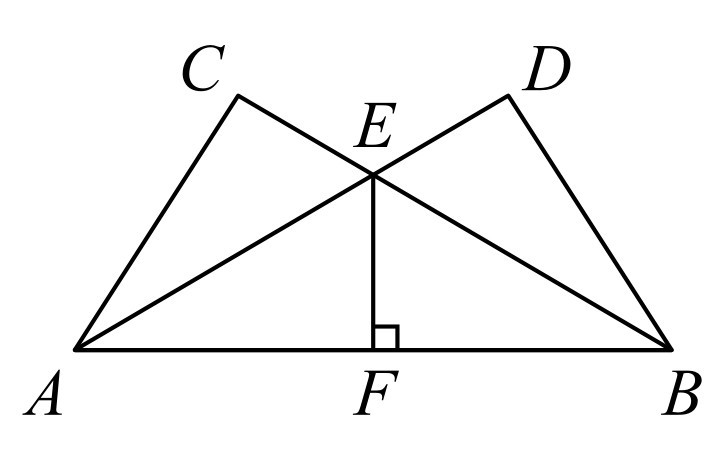
图4-6
【解析】
设∠EAB=α，∠EBA=β，则有Rt△AFE，Rt△ABC，Rt△BFE和Rt△ADB中，
，BC=AB·cosβ，
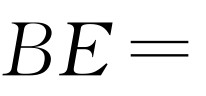
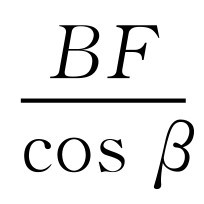，AD=AB·cosα，所以
.
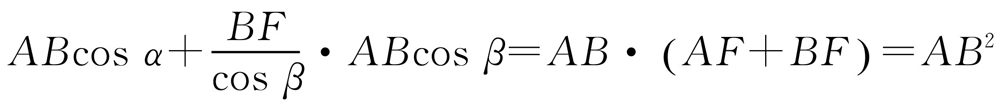（☆☆）【4.2.3】
如图4-7所示，在△ABC中，AC＞BC，AD⊥BC，BE⊥AC，点D，E分别为垂足．求证：AC+BE≥BC+AD.
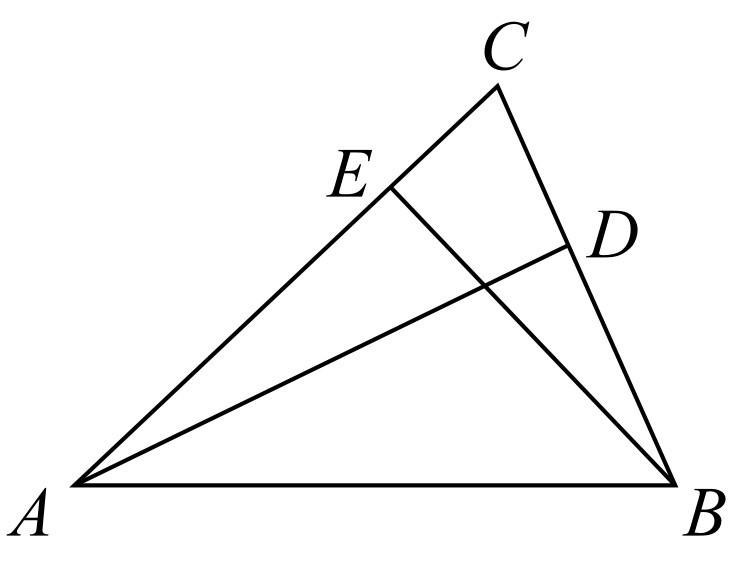
图4-7
【解析】
设AC=b，BC=a，则b＞a.
在Rt△ADC和Rt△CEB中，有AD=b·sin C，BE=a·sin C.
因为0°＜C＜180°，所以0＜sin C≤1，
所以AD-BE=（b-a）sin C≤b-a=AC-BC.
故AC+BE≥AD+BC，其中当且仅当∠C=90°时等号成立．
（☆☆☆）【4.2.4】
如图4-8所示，正方形ABCD的边长是2，M是AD的中点，点E从点A出发，沿AB运动到点B停止，连接EM并延长交射线CD于点F，过M作EF的垂线交射线BC于点G，连接EG，FG.
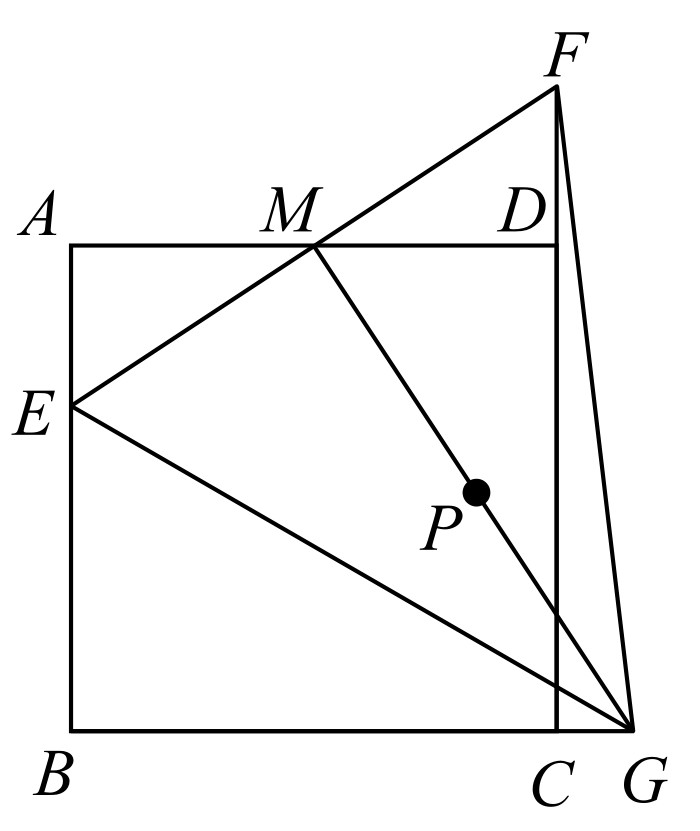
图4-8
（1）设AE=x时，△EGF的面积为y，求y关于x的函数关系式，并填写自变量x的取值范围．
（2）P是MG的中点，请直接写出点P运动路线的长．
【解析】
（1）当点E与点A重合时，x=0，
；当点E与点A不重合时，0＜x≤2．在正方形ABCD中，∠A=∠ADC=90°，所以∠MDF=90°，所以∠A=∠MDF．因为AM=DM，∠AME=∠DMF，所以△AME≌△DMF，ME=MF.
在Rt△AME中，AE=x，AM=1，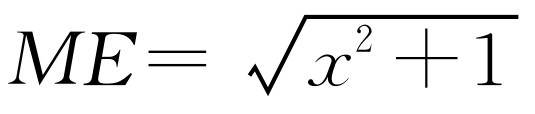
，所以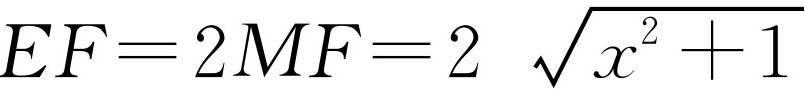
.
如图4-9所示，过点M作MN⊥BC．则∠MNG=90°，∠AMN=90°，MN=AB=AD=2AM，所以∠AME+∠EMN=90°．因为∠EMG=90°，所以∠GMN+∠EMN=90°，∠AME=∠GMN，Rt△AME∽Rt△NMG．所以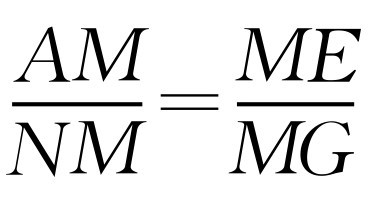
，即
.所以
.所以
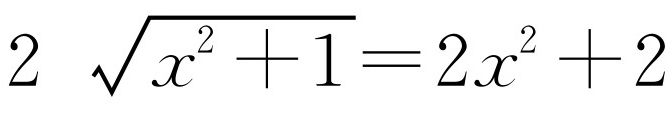．所以y=2x2+2，其中0≤x≤2.
图4-9
（2）点P运动路径的长为2.
【备注】
点P运动轨迹是一条直线，所以以B为坐标轴原点，以BC为x轴正方向，以BA为y轴正方向建立坐标系，只需分别求出当E与A重合、当E与B重合时点P的坐标，再求两点间距离即可．
（☆☆）【巩固练习2】
如图4-10所示，△ABC为等边三角形，边长为a，DF⊥AB，EF⊥AC，已知A，D，F，E四点共圆，已知
，求此圆直径．
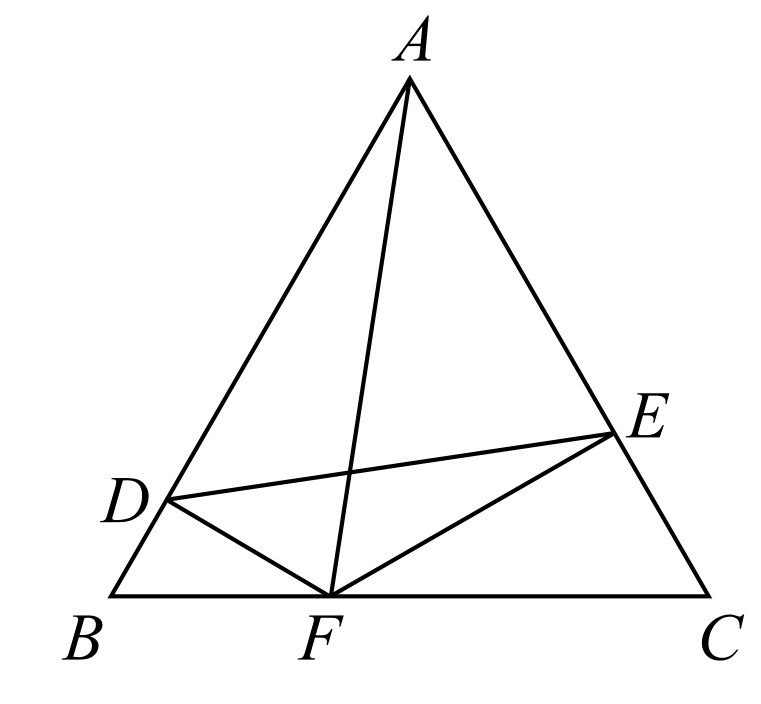
图4-10