【典型应用4】综合应用
（☆☆☆）【2.4.1】
如图2-10所示，已知抛物线的方程C1：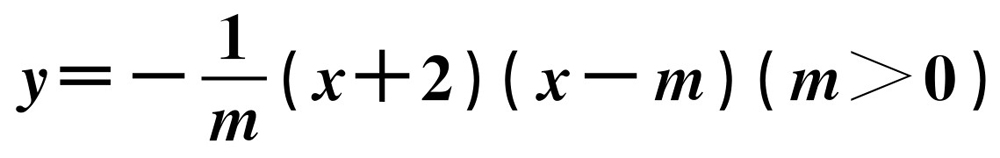
与x轴交于点B，C，与y轴交于点E，且点B在点C的左侧．
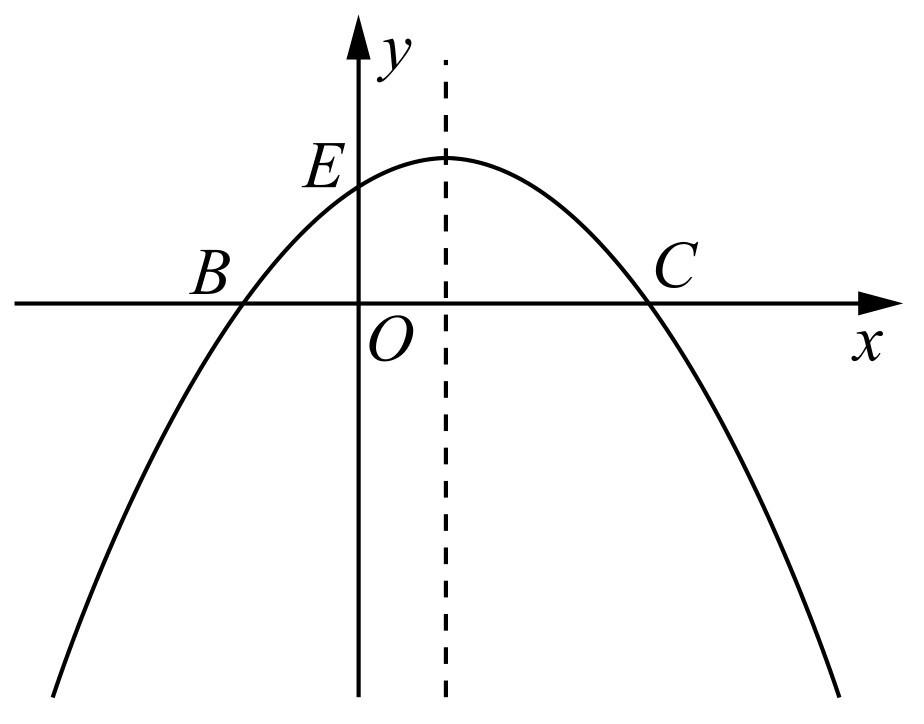
图2-10
（1）若抛物线C1过点M（2，2），求实数m的值．
（2）在（1）的条件下，求△BCE的面积．
（3）在（1）的条件下，在抛物线的对称轴上找一点H，使得BH+EH最小，求出点H的坐标．
（4）在第四象限内，抛物线C1上是否存在点F，使得以点B，C，F为顶点的三角形与△BCE相似？若存在，求m的值；若不存在，请说明理由．
【解析】
（1）将M（2，2）代入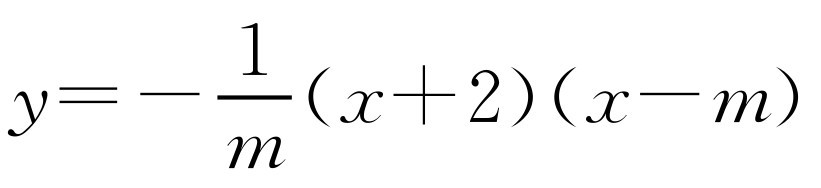
，得
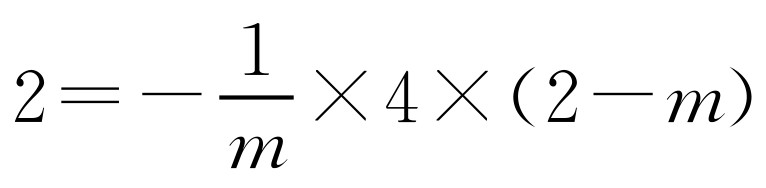．解得m=4.
（2）当m=4时，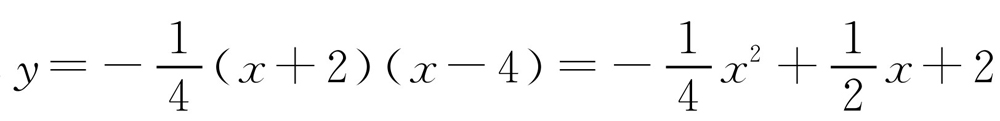
．所以B（-2，0），C（4，0），E（0，2）.
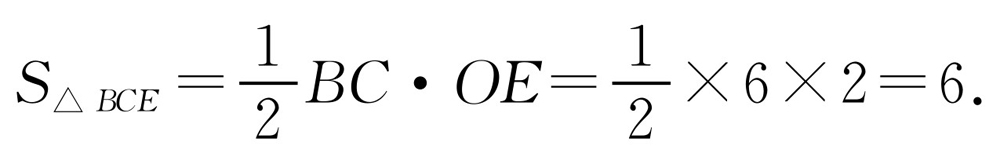
（3）如图2-11所示，抛物线的对称轴是直线x=1，当点H落在线段EC上时，BH+EH最小．设对称轴与x轴的交点为P，那么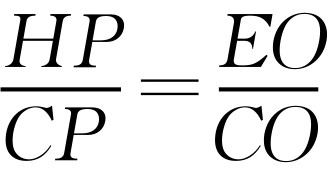
．因此
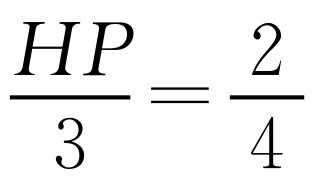．解得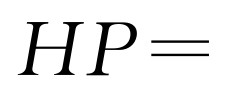
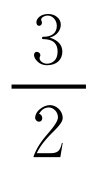.所以点H的坐标为
.
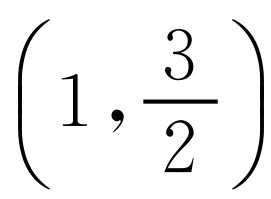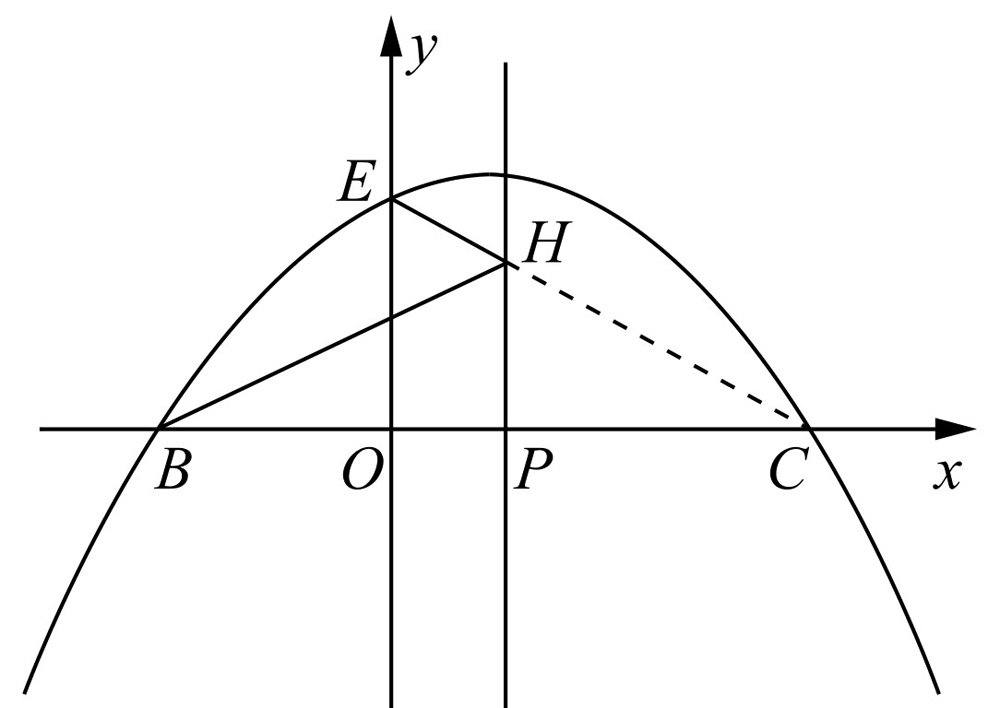
图2-11
（4）①如图2-12所示，过点B作EC的平行线交抛物线于点F，过点F作FF′⊥x轴于F′．由于∠BCE=∠FBC，所以当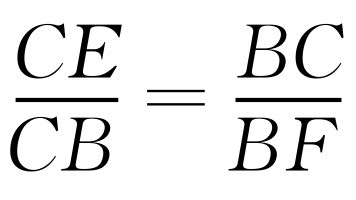
，即BC2=CE·BF时，△BCE∽△FBC．设点F的坐标为
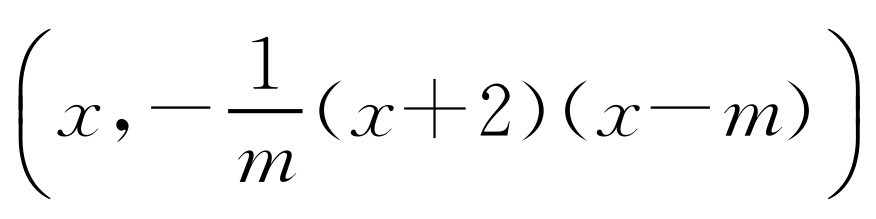，由
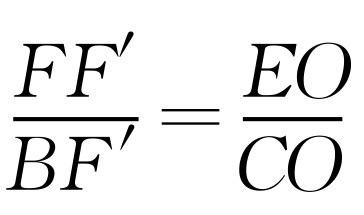，得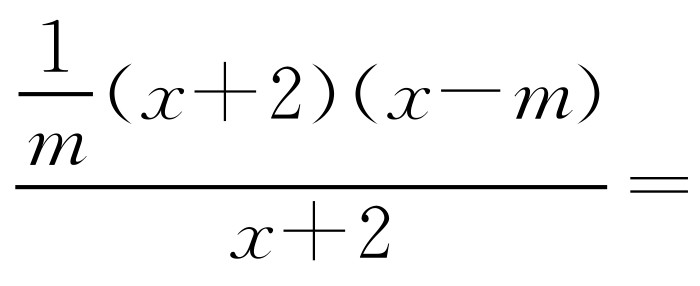
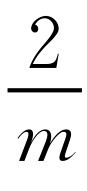.解得x=m+2．所以F′（m+2，0）．由
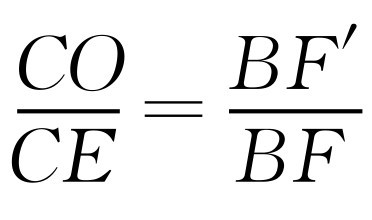，得
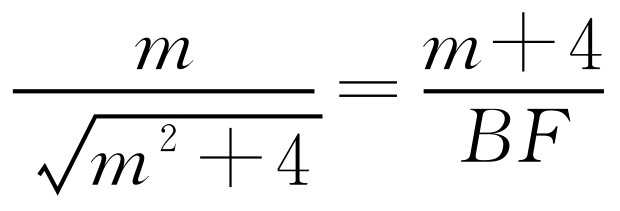.所以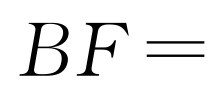
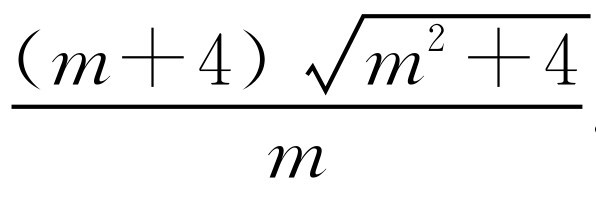.由BC2=CE·BF，得
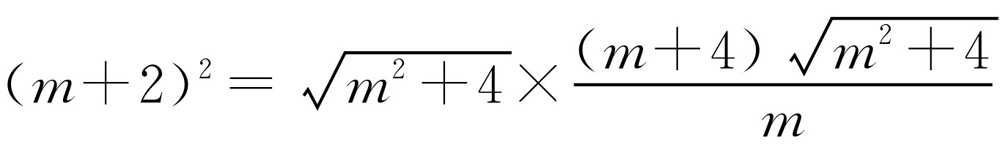.整理得0=16．此方程无解．
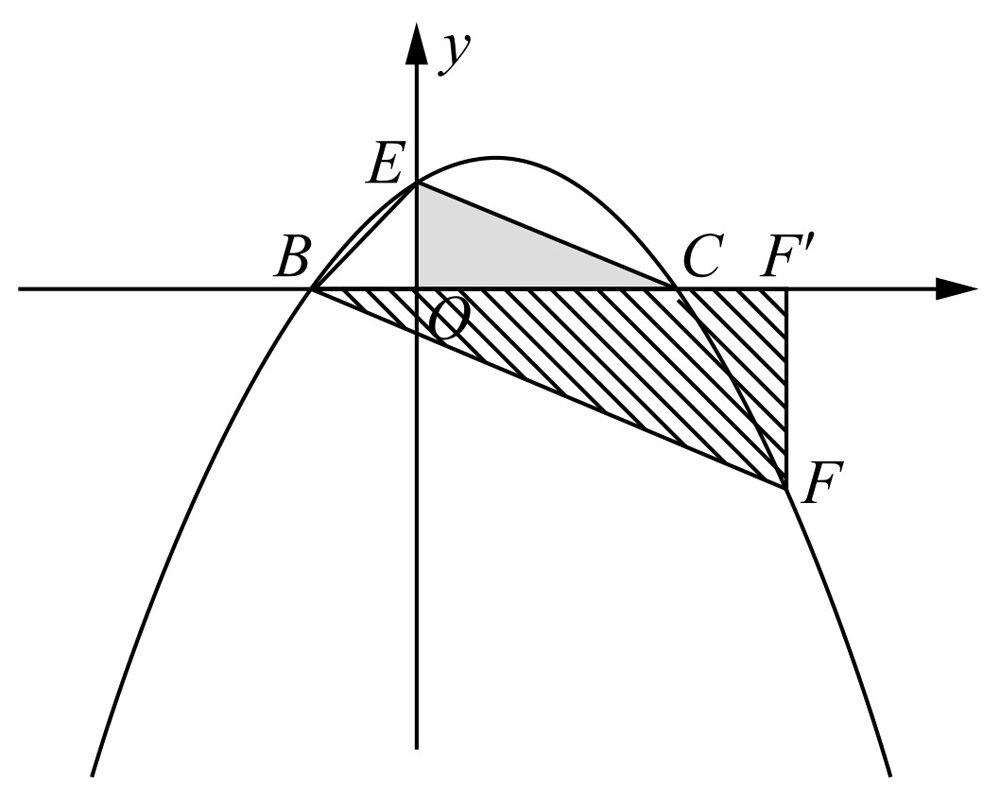
图2-12
②如图2-13所示，作∠CBF=45°交抛物线于点F，过点F作FF′⊥x轴于F′，由于∠EBC=∠CBF，所以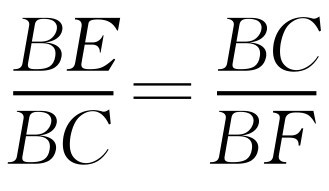
，即BC2=BE·BF时，△BCE∽△BFC．在Rt△BFF′中，由FF′=BF′，得
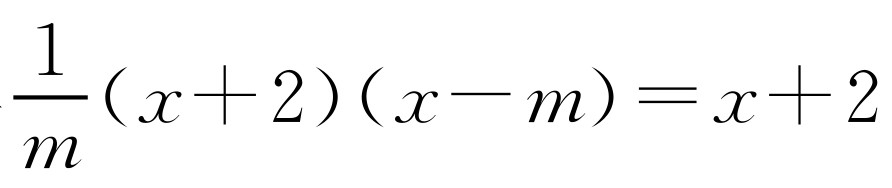.解得x=2m．所以F′（2m，0）．所以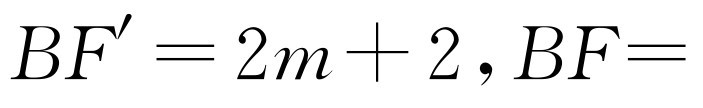
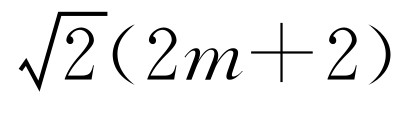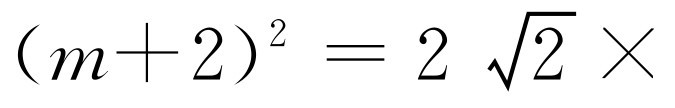
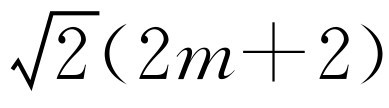．由BC2=BE·BF，得
．解得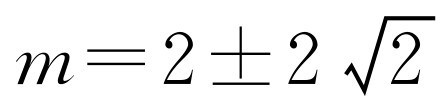
.
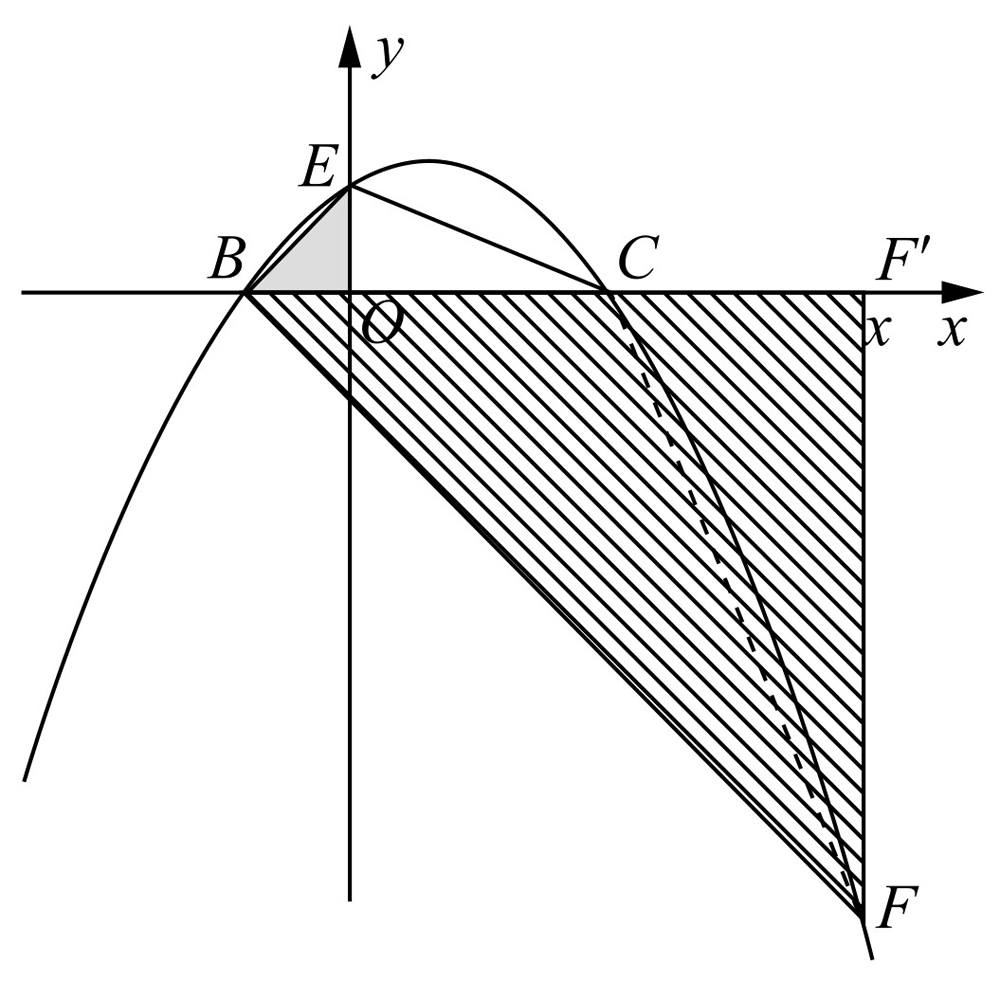
图2-13
综合①②，符合题意的m为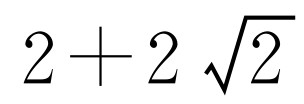
.
（☆☆☆）【2.4.2】
如图2-14所示，抛物线经过点A（4，0），B（1，0），C（0，-2）三点．
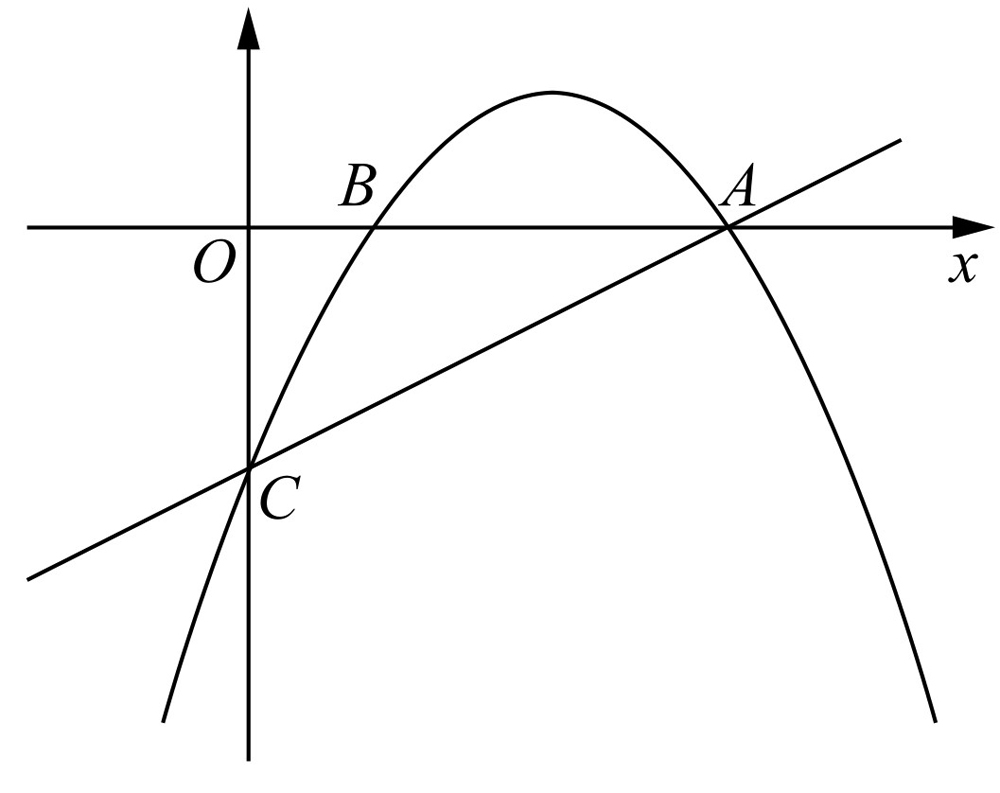
图2-14
（1）求此抛物线的解析式．
（2）点P是抛物线上的一个动点，过点P作PM⊥x轴，垂足为点M，是否存在点P，使得以A，P，M为顶点的三角形与△OAC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．
（3）在直线AC上方的抛物线是有一点D，使得△DCA的面积最大，求出点D的坐标．
【解析】
（1）因为抛物线与x轴交于A（4，0），B（1，0）两点，设抛物线的解析式为y=a（x-1）（x-4），代入点C的坐标（0，-2），解得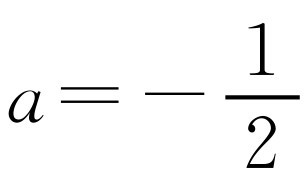
．所以抛物线的解析式为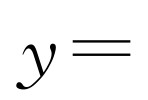
.
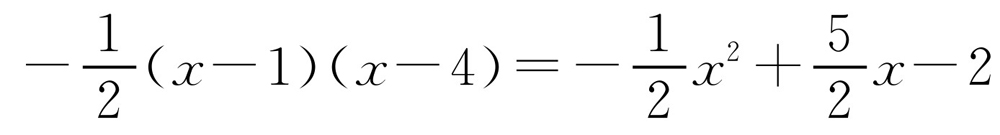（2）设点P的坐标为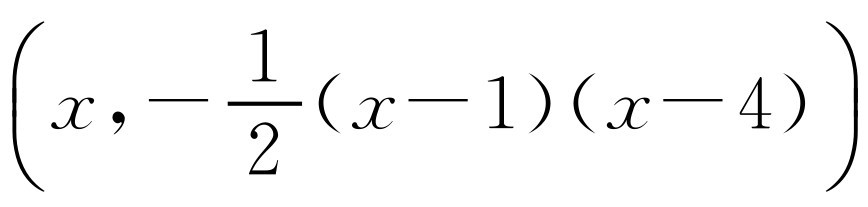
.
①如图2-15所示，当点P在x轴上方时，1＜x＜4，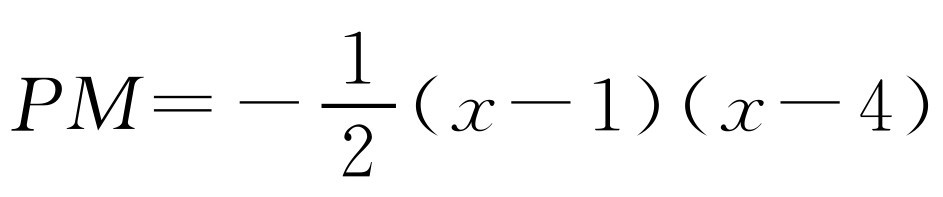
，AM=4-x．如果
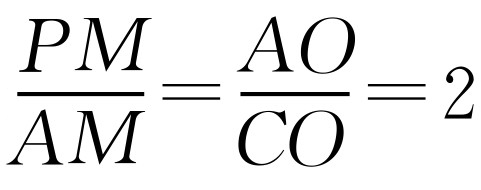，那么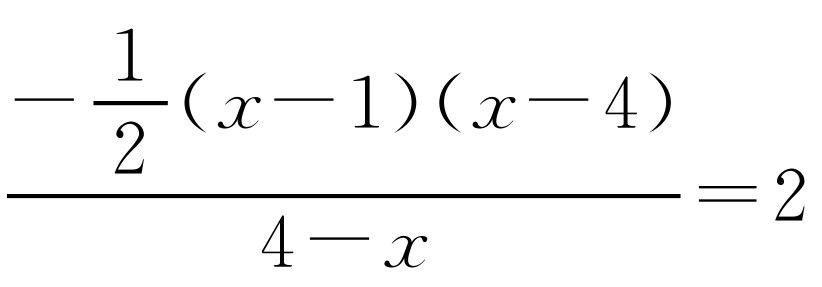
.解得x=5不合题意．如果
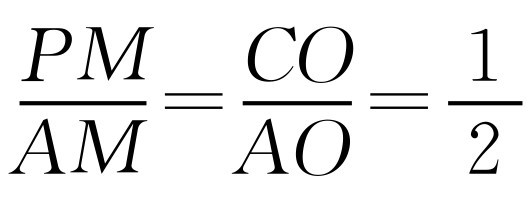，那么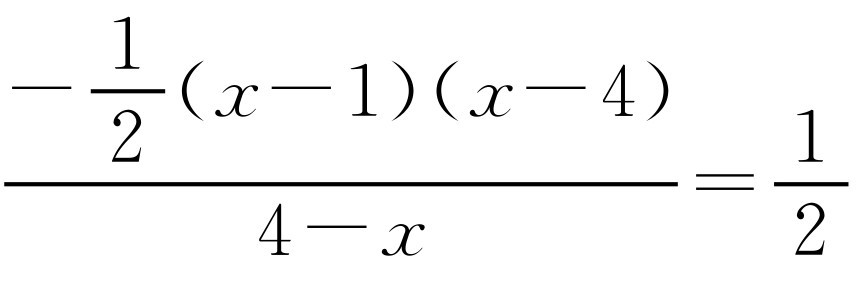
.解得x=2．此时点P的坐标为（2，1）.
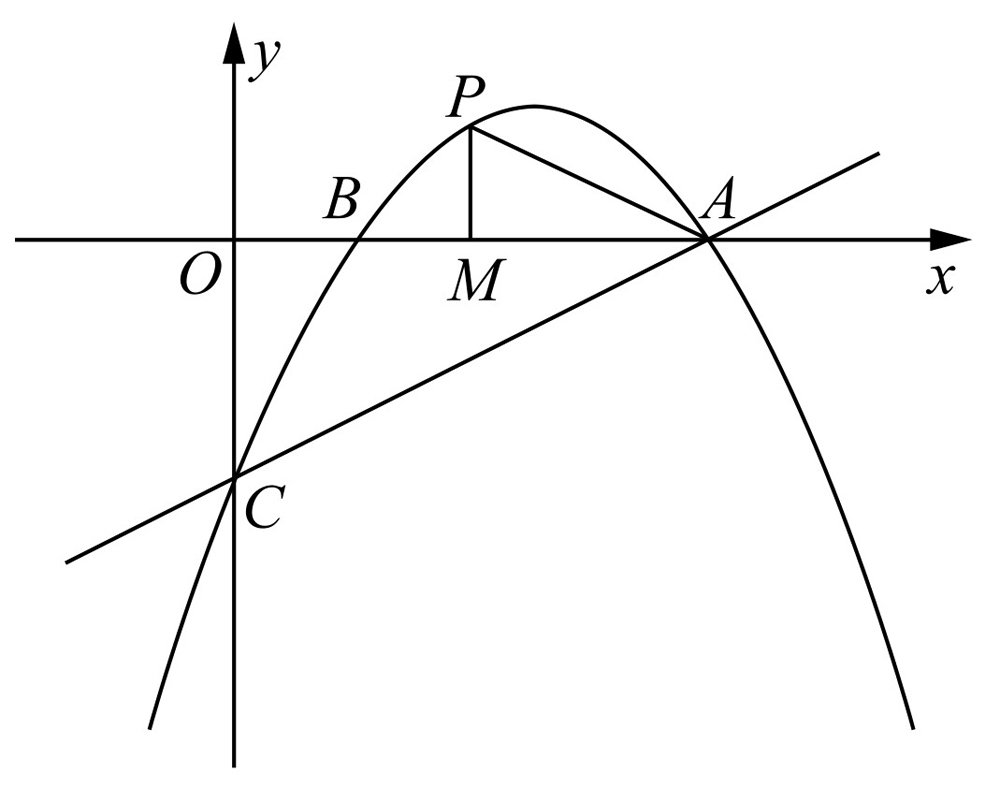
图2-15
②如图2-16所示，当点P在点A的右侧时，x＞4，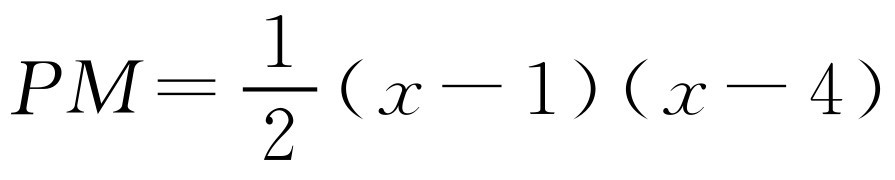
，AM=x-4．解方程
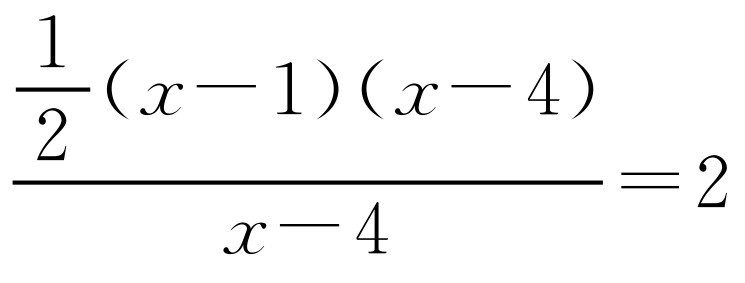，得x=5，此时点P的坐标为（5，-2）．解方程
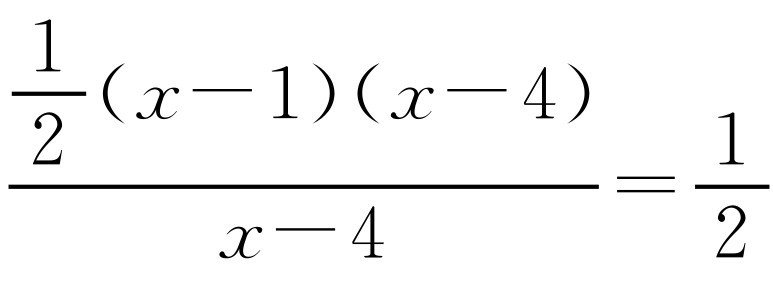，得x=2，不合题意．
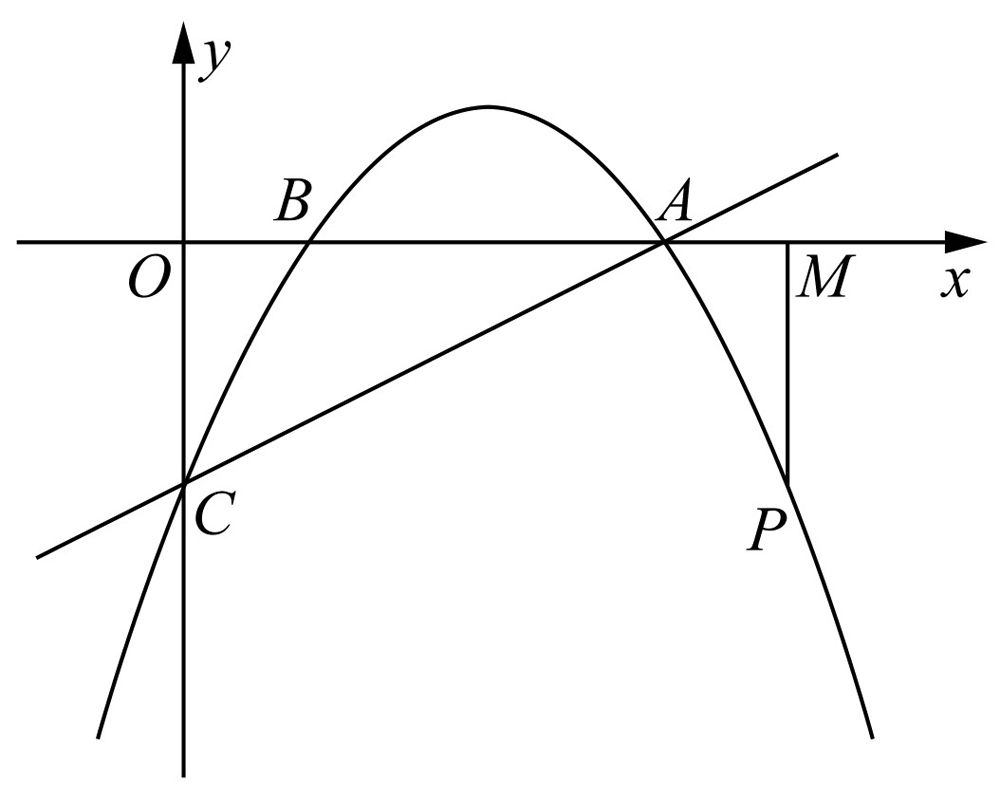
图2-16
③如图2-17所示，当点P在点B的左侧时，x＜1，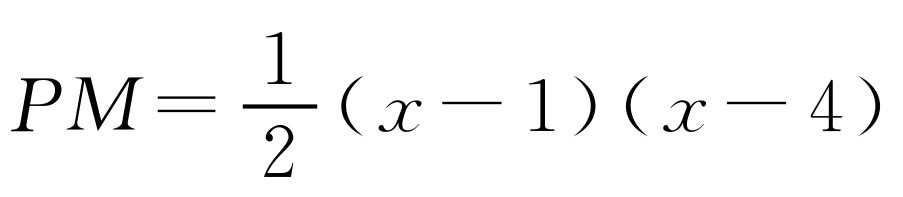
，AM=4-x．解方程
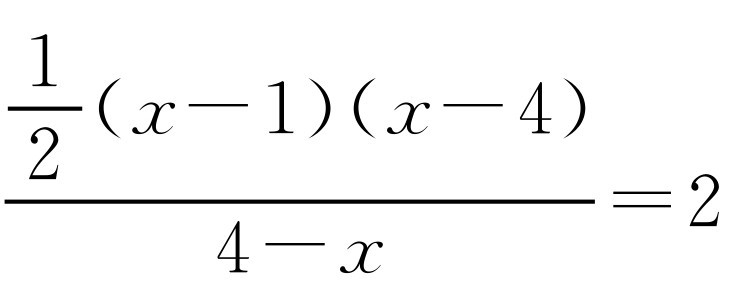，得x=-3．此时点P的坐标为（-3，-14）.解方程
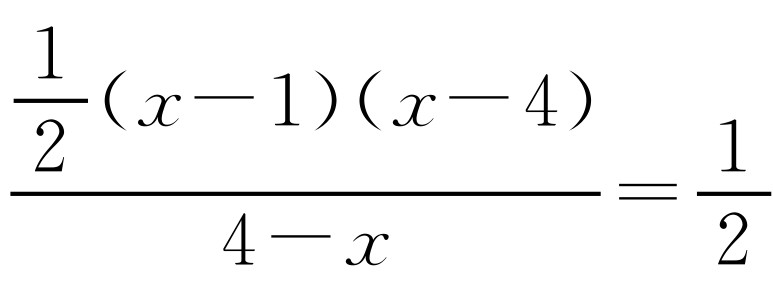，得x=0．此时点P与点O重合，不合题意．
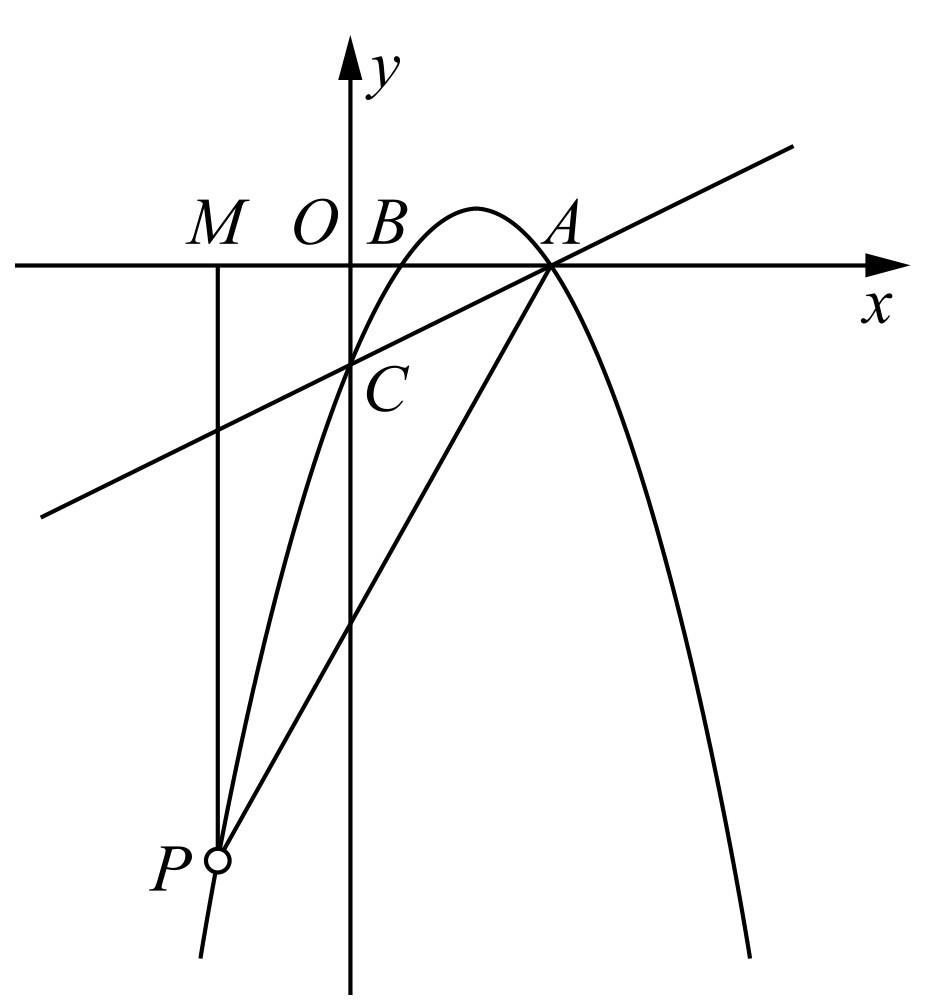
图2-17
综上所述，符合条件的点P的坐标为（2，1）或（-3，-14）或（5，-2）.
（3）如图2-18所示，过点D作x轴的垂线交AC于E．直线AC的解析式为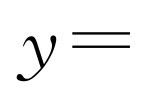
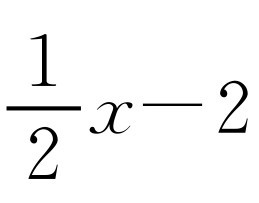.设点D的横坐标为m（1＜m＜4），那么点D的坐标为
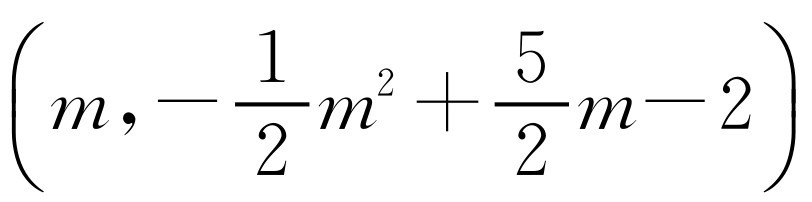，点E的坐标为
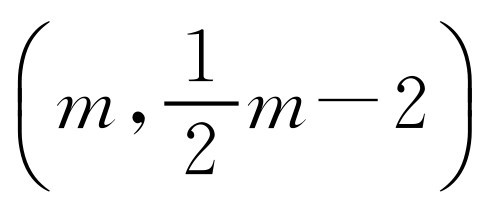.所以
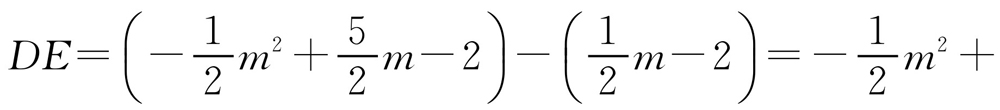
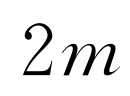．因此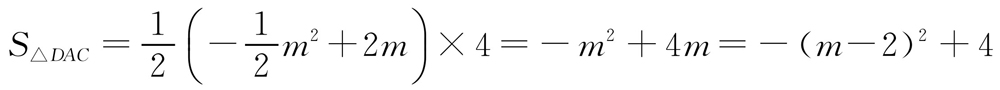
.当m=2时，△DCA的面积最大，此时点D的坐标为（2，1）.
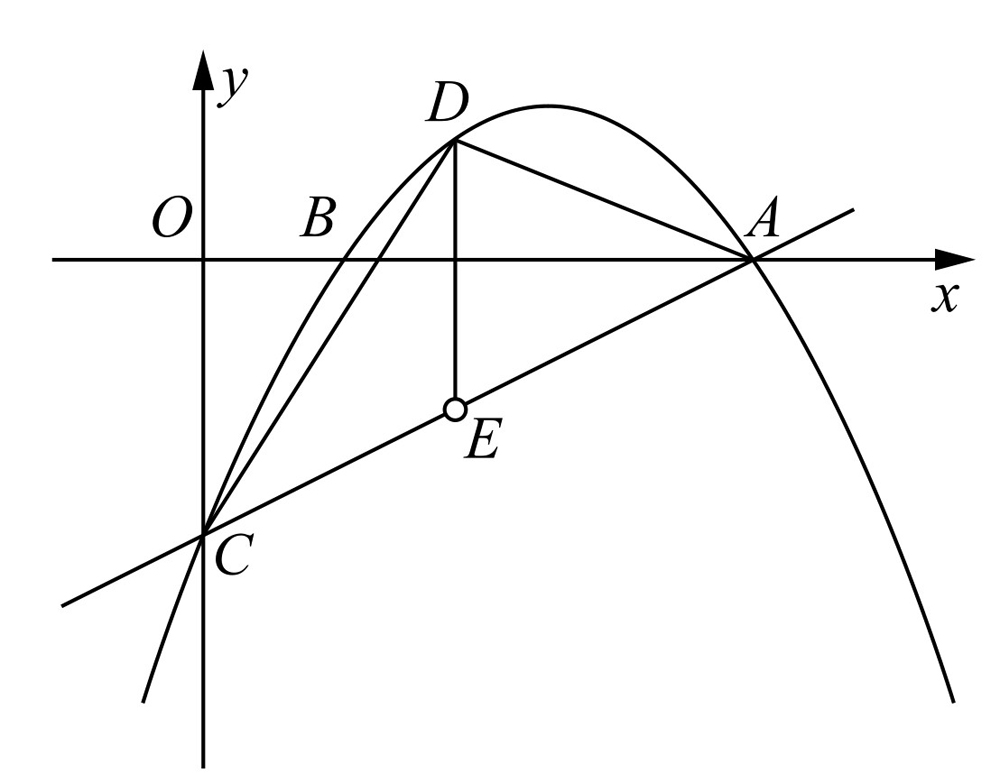
图2-18
【巩固练习4】
如图2-19所示，点A在x轴上，OA=4，将线段OA绕点O顺时针旋转120°至OB的位置．
图2-19
（1）求点B的坐标．
（2）求经过A，O，B的抛物线的解析式．
（3）在此抛物线的对称轴上，是否存在点P，使得以点P，O，B为顶点的三角形是等腰三角形？若存在，求点P的坐标；若不存在，请说明理由．