凯利公式最初是为AT&T贝尔实验室物理学家约翰·拉里·凯利根据同事克劳德·艾尔伍德·香农于长途电话线杂讯上的研究所建立。凯利公式之所以著名,就是被凯利的另一名同事索普应用于BlackJack和股票交易中的。
但BlackJack和股票市场有着本质的不同,BlackJack游戏输赢是有比例的,或1赔1,或1赔1.5。但股票市场可不一定,赚钱还是不赚钱,不是靠着准确率,这一点你看一下海龟法则的回测数据就可以知道了。除了准确率,还要看盈亏比。盈亏比就是关键,问题也就出在这里,交易中盈亏比是不确定的。
可我们的回测数据不是给出了盈亏比数据吗?不能直接用吗?可以用,但并不保险。盈比亏随着交易的不断进行会发生变化,虽然变化很细微,那是因为大量的交易平均化的结果。而单次盈亏比或大或小,若突然出现一次非常大的单次盈亏比,平均盈亏比基本不会变化太多,但对于持仓规模较大的交易,损失可就大了。
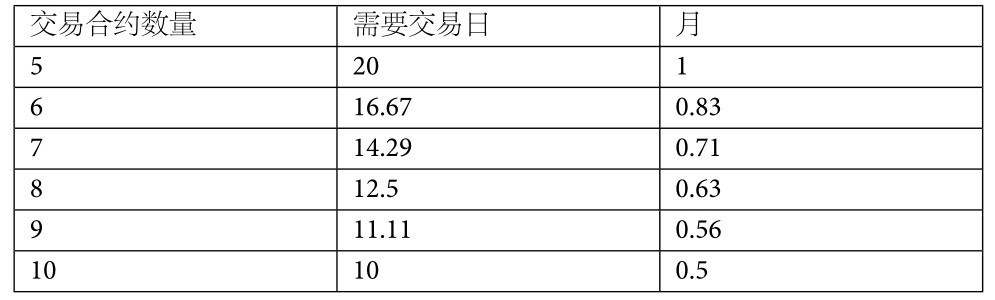
假设你现在有10000元,可以做1手,1天赚100元,1个月20个交易日, 1个月赚2000元。那么你赚到下一个10000元,需要100个交易日,5个月的时间。此时你的资金达到20000元,交易量可以达到2手,每天就会赚200元,只需要50个交易日,2.5个月的时间。这样增加交易手数的时间越来越快。如表8-1所示。
表8-1 每增加一手合约数量所需要的时间

(续表)
《短线交易秘诀》的作者Larry Williams给了一个非常形象的比喻,最开始只拥有1手合约的时候你坐在树根,当你不停赚了1万元就加一倍持仓的话,树枝不断地分杈,你越坐越高。但是树杈越分越细,而你交易的合约越来越多。只要输掉一笔,你就会听到树枝清脆的折断声。
若每笔亏损也是100元的话,你交易10手,就要损失1000元。你赚的时候只赚1%,但是1笔亏损就是10%,赚1亏10,可不是一笔好生意。这就是在交易中使用凯利公式的弊端。
按上面的例子,资金使用率为34.34%,也就是你用10000元中的3434元进行交易。平均盈亏比是1.58,那么你一笔交易平均赚5425.72元。此时你已经有了15425.72元了,再用34.34%的资金——5297.19元交易,再赚一次,你将得到8368.52元。如表8-2所示。
表8-2 应用凯利公式的资金管理 单位:元
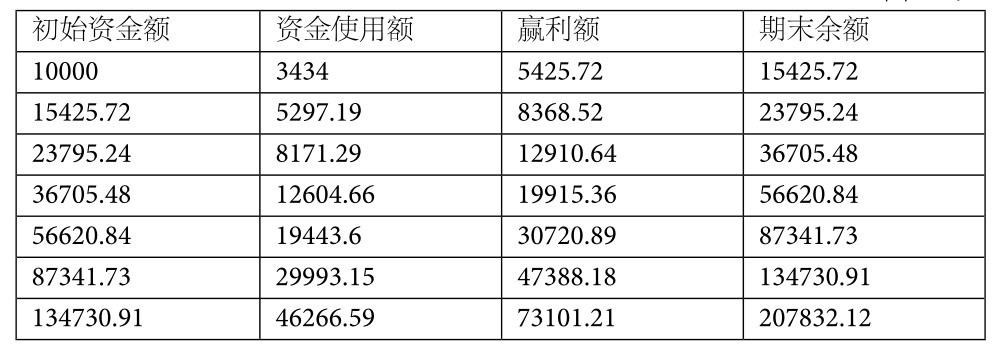
你只进行了7笔交易,就从1万元变成了20.78万元,是不是很痛快?盈亏比是1.58的话,那么亏盈比就是1.58的倒数0.63。当你有了20.78万元的时候,拿出34.34%进行交易,就是71368.55元。亏损的百分比是63%,只要错一次就要亏损44962.82元。现在剩多少钱了呢?162868.3元(207832.12-44962.82)。
我们再拿出34.34%的钱55928.32元来,再亏一次63%,35235.47元,本金剩余127633.83元。赚了7次,亏了2次,共亏损80198.29元(207832.12-127633.83)。亏损了38.59%(80198.29/207832.12)。
这么算来,RangeBreak系统的胜率高达58.78,而盈亏比也达到了1.58。仅从这两组数据来看,这绝对是一个非常优秀的交易系统。但我们模拟了9笔交易,赚7笔,亏2笔,准确率达到77.78%,盈亏比未变还是1.58。亏损幅度竟然高达38.59%,这么大的亏损幅度,对任何一个系统来说,都不是一个好兆头。
你可能会说,如果先亏后赚,亏损幅度就不会那么高了,好,我们再算一算。其他条件不变,10000元中拿出3434元进行交易,亏损63%,亏损2163.42元,本金剩余7836.58元。再拿出34.34%,2691.08元。再亏损一次63%,亏损1695.38元。此时总亏损3858.8元,亏损幅度38.59%。两组数据是一致的,不论你如何交易,在我们设定的77.78%准确率的情况下,总亏损幅度还是一样大。
看来凯利公式只能用于基于算牌法的BlackJack游戏中,而不适用于股票交易。这个问题还告诉我们,加仓时不能直接按照赚了多少钱就相应加多少仓来计算。那我们除了凯利公式还能用什么呢?