5.1.2 数制和编码
本节主要介绍数制的概念和各种数制之间的转换,以及西文字符的编码和汉字的编码。
1.进制的表示
在日常生活中,用十进制来表示数已经广泛被人们所接受。但是由于计算机底层使用的电路硬件通常只能够清晰地表示两种状态,即开和关,或者说高电平和低电平。如果使用十进制,将会使得计算机底层的设计变得过于复杂,而且容易出错,因此通常采用二进制来表示数。
二进制数比较长,也比较容易看错,不便于人们进行思考和操作,所以通常采用八进制和十六进制来解决这个问题,八进制和十六进制的表示方法既缩短了二进制数的位数,又保留了二进制数的表达特点。
R进制,通常的说法就是逢R进1,可以用的数为R个,分别是0、1、2、…、R-1。例如八进制数的基数为8,即可以用到的数码个数为8,它们是0、1、2、3、4、5、6以及7;二进制数的基数为2,可用的数码个数为2,它们是0和1。对于十六进制,它的数码为0、1、2、3、4、5、6、7、8、9、A、B、C、D、E以及F。
为了把不同的进制数分开表示,避免造成混淆,通常采用下标的方式来表示一个数的进制,如十进制数88表示为(88) 10 ,八进制数76表示为(76) 8 。在计算机专业术语的表达中,通常在数字的后面加大写的“H”表示十六进制,例如FCH就表示十六进制数FC。
(1)R进制数与十进制数的转换
对于任意一个R进制数,它的每一位数值等于该位的数码乘以该位的权数。权数由一个幂Rk表示,即幂的底数是R,指数为k,k与该位和小数点之间的距离有关。当该位位于小数点左边时,k值是该位和小数点之间数码的个数,而当该位位于小数点右边时,k值是负值,其绝对值是该位和小数点之间数码的个数加1。
例如,八进制数234.56,其数值可计算如下。
234.56=2×82 +3×81 +4×80 +5×8-1 +6×8-2 =128+24+4+5/8+6/64=156.71875
又如,二进制数10100.01的值可计算如下。
10100.01=1×24 +1×22 +1×2-2 =16+4+0.25=20.25
按照上面的表示法,即可计算出R进制数转换成十进制数的值。
十进制整数转换成R进制数,最常用的是“除以R取余法”。例如,将十进制数94转换为二进制数计算如下。

将所得的余数从低位到高位排列,得到(1011110) 2 就是94的二进制数。
十进制小数转换为R进制小数,则采用“乘以R取进位法”。例如,将十进制小数0.43转换成二进制小数的过程如下(假设要求小数点后取5位)。

即转换后的二进制小数为(0.01101) 2 。
(2)二进制数与八进制数的转换
将二进制数转换为八进制数,以小数点为分界线,分别从右到左(整数部分)和从左到右(小数部分),将每3位二进制数转换为八进制数即可,最后不足3位的,则在最高位补0(整数部分)或最低位补0(小数部分)。
例如,二进制数1011110转换为八进制数,则可以分为3段(001,011,110),其对应的八进制数为(1,3,6),因此,(1011110) 2 =(136) 8 。
又如,二进制数10100.0101转换为八进制数,则需要在整数部分的最高位补1个0,在小数部分的最低位补2个0,然后分为4段(010,100,010,100),其对应的八进制数为(2,4,2,4),因此,(10100.0101) 2 =(24.24) 8 。
相反,将八进制数转换为二进制数,只要将每位八进制数转换为3位二进制数即可。
例如,八进制数56.23转换为二进制数,因为5=(101) 2 ,6=(110) 2 ,2=(010) 2 ,3=(011) 2 ,所以(56.23) 8 =(101110.010011) 2 。
(3)二进制数与十六进制数的转换
将二进制数转换为十六进制数,以小数点为分界线,分别从右到左(整数部分)和从左到右(小数部分),将每4位二进制数转换为十六进制数即可,最后不足4位的,则在最高位补0(整数部分)或最低位补0(小数部分)。
例如,二进制数1011110转换为十六进制数,可以分为2段(0101,1110),其对应的十六进制数为(5,E),因此,(1011110) 2 =5EH。
又如,二进制数110100.10111转换为十六进制数,则需要在整数部分的最高位补2个0,在小数部分的最低位补3个0,然后分为4段(0011,0100,1011,1000),其对应的十六进制数为(3,4,B,8),因此,(110100.10111) 2 =34.B8H。
相反,将十六进制数转换为二进制数,只要将每位十六进制数转换为4位二进制数即可。
例如,十六进制数D6.C3H转换为二进制数,因为D=1101,6=0110,C=1100,3=0011,所以D6.C3H=(11010110.11000011) 2 。
2.数据的表示
本小节主要介绍数的表示(原码、反码、补码表示法,整数和实数的机内表示)、非数值表示(字符和汉字表示、声音表示、图像表示)。
(1)数值的编码表示
主要要求掌握原码、反码、补码和移码的概念和特点。
1)原码
原码表示法是在数值前面增加了一位符号位(即最高位为符号位),该位为0时表示正数,为1时则表示负数,其余各位表示数值的大小。这种方式简单直观,也是最容易理解的。
例如,假设用8位表示一个数字,则+11的原码是00001011,-11的原码是10001011。其缺点就是原码直接参加运算可能会出现错误的结果。例如,(1) 10 +(-1) 10 =0,如果直接使用原码,则(00000001)2+(10000001) 2 =(10000010) 2 ,这样计算的结果是-2,显然出错了。所以,原码的符号位不能直接参与计算,必须和其他位分开,这样会增加硬件的开销和复杂性。
2)反码
反码表示法和原码表示法一样是在数值前面增加了一位符号位(即最高位为符号位),正数的反码与原码相同,负数的反码符号位为1,其余各位为该数绝对值的原码按位取反。
例如,+11的反码是00001011,-11的反码为11110100。
同样,对于(1) 10 +(-1) 10 =0,如果使用反码,则(00000001) 2 +(11111110) 2 =(11111111) 2 ,结果为负0,而在人们的观念中,0是不分正负的。反码的符号位可以直接参与计算,而且减法也可以转换为加法运算。
注意:用反码进行两数相加时,若最高位有进位,还必须把该进位值加到结果的最低位,才能得到真正的结果,这一操作通称为“循环进位”。
3)补码
补码表示法和原码表示法一样是在数值前面增加了一位符号位(即最高位为符号位),正数的补码与原码相同,负数的补码是该数的反码加1,这个加1就是“补”。
例如,+11的补码是00001011,-11的补码为11110101。
同样,对于(1) 10 +(-1) 10 =0,如果使用补码,则(00000001) 2 +(11111111) 2 =(00000000) 2 ,直接使用补码计算的结果是正确的。也就是说,补码中0是唯一表示的。
在大部分的计算机系统中,数据都使用补码表示,因为采用补码能使符号位与有效值部分一起参加运算,从而简化了运算规则,同时它也使减法运算转换为加法运算,硬件电路只需要设计加法器。
4)移码
移码又称为增码,一般用来表示浮点数的阶码,其定义为[X]移=2n +X(-2n ≤X≤2n )。
移码的符号位表示和补码相反,1表示正数,0表示负数。
(2)非数值的编码表示
计算机除了处理数值信息以外,还要处理大量的非数值类型的信息,比如字母、汉字、声音、图像等,然而计算机只能处理二进制数据,当这些非数值类型的信息应用在计算机内,都必须转换为二进制的表现形式。
1)ASCII码
为了表示英文字母和其他一些符号、控制符,计算机中普遍采用的是ASCII码。它使用7位代表一个字符,包括了字母的大小写、数字、标点、控制符等。计算机通常使用8位一个字节来存储,其高位为0。表5-1列出了全部128种字符的ASCII码字符编码。
表5-1 ASCII码表

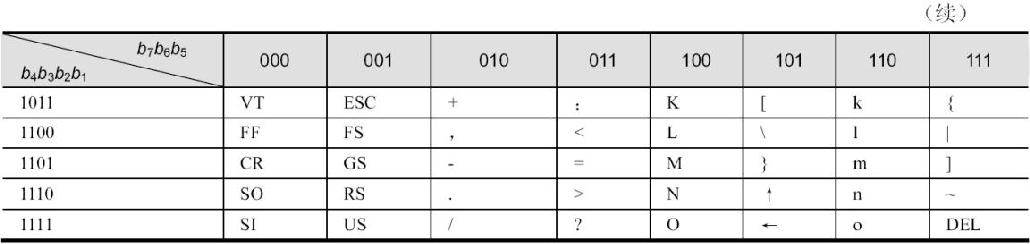
2)汉字编码
汉字与西方字符相比,汉字数量大、字形复杂、同音字多,这就给汉字在计算机内部的存储、传输、交换、输入、输出等带来了一系列的问题。为了能直接使用西文标准键盘输入汉字,必须为汉字设计相应的编码,以适应计算机处理汉字的需要。表5-2列出了常见的汉字字符编码。
表5-2 常见的汉字字符编码
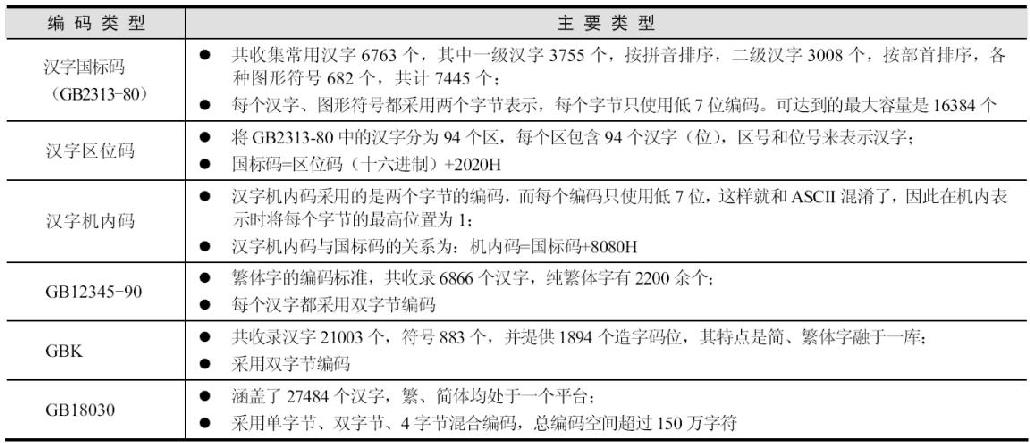
3)声音编码
声音本身是模拟信息,在计算机中表示模拟量必须将模拟量进行数字化,数字化遵循采样定理。
在实践中,通常使用三个参数来表示声音:采样位数、采样频率和声道数。声道有单声道和立体声之分,甚至更多。人能听见的声音的最高频率是20kHz,根据采样定理,44100Hz(44kHz)的采样频率能够很好地还原各种声音,而普通人的声带能够达到4000Hz,所以8kHz的采样频率能够满足语言采样的需要。其他采样频率有11025Hz(11kHz)、22050Hz(22kHz)等,能够适合不同的场景。采样位数是每个采样点采用多少位来保存声音的强度值,采样位数越高,则还原时越精确。如果不采用压缩技术,那么保存声音需要的空间算式为文件所占容量=(采样频率×采样位数×声道)×时间/8(1字节 =8bit)。
目前主要的音频数据格式如下。
·WAVE(扩展名为WAV):该格式记录声音的波形,故只要采样频率高、采样字节长、机器速度快,利用该格式记录的声音文件就能和原声基本一致,而且质量非常高,但这样做的代价就是文件太大。
·MOD(扩展名为MOD、ST3、XT、S3M、FAR、669等):该格式的文件里存放乐谱和乐曲使用的各种音色样本,具有回放效果明确、音色种类无限等优点。但它也有一些致命弱点,以至于现在已经逐渐被淘汰,目前只有MOD迷及一些游戏程序中尚在使用。
·Layer-3(扩展名为MP3):现在最流行的声音文件格式,因其压缩率大,在网络可视电话通信方面应用广泛,但和CD唱片相比,音质不能令人非常满意。Layer-3是MPEG标准的一部分,是一种强有力的音频编码方案。Layer-3在现存的MPEG-1和MPEG-2国际标准的音频部分上均有定义,简称MP3(MPEG AudioLayerⅢ)。
·Real Audio(扩展名为RA):这种格式具有强大的压缩量和极小的失真使其在众多格式中脱颖而出。和MP3相同,它也是为了解决网络传输带宽资源而设计的,因此主要目标是压缩比和容错性,其次才是音质。
·CD Audio(音乐CD,扩展名为CDA):唱片采用的格式,又叫“红皮书”格式,记录的是波形流,绝对的纯正、HIFI。但缺点是无法编辑,文件长度太大。
·MIDI(扩展名为MID):作为音乐工业的数据通信标准,MIDI能指挥各音乐设备的运转,而且具有统一的标准格式,能够模仿原始乐器的各种演奏技巧甚至一些无法演奏的效果。MIDI文件是按照MIDI标准制成的声音文件,其文件记录声音的方法与WAV完全不同,它并不记录对声音的采集数据,而是记录编曲的音符、音长、音量和击键力度等信息,相当于乐谱。由于MIDI文件记录的不是乐曲本身,而是一些描述乐曲演奏过程中的指令,因此它占用的存储空间比WAV文件小很多,即使是长达十多分钟的音乐最多也不过几十 KB。
·Creative Musical Format(扩展名为CMF):Creative公司的专用音乐格式,和MIDI差不多,只是音色、效果上有些特色,专用于FM声卡,但其兼容性很差。
4)图像编码
图像也称为位图或点阵图,是指由输入设备捕捉的实际场景画面或以数字化形式存储的任意画面。图像都是由一些排成行列的像素组成的,它除了可以表现真实的照片,也可以表现复杂绘画的某些细节,并具有灵活和富于创造力等特点。
图像的主要指标有分辨率、点距、深度(灰度)。
·分辨率:可以分为屏幕分辨率和输出分辨率。屏幕分辨率是指每英寸的点阵的行数或列数,这个数值越大,表示就越好。输出分辨率是指每英寸的像素点数,是衡量输出设备的精度,数值越大,质量越好。
·点距:指两个像素之间的距离,一般来说,分辨率越高,则像素点距的规格越小,显示效果越好。
·深度:图像深度确定彩色图像的每个像素可能有的颜色数,或者确定灰度图像的每个像素可能有的灰度级数。通常,图像深度也指存储每个像素所用的存储器位数,或者说用多少位存储器单元来表示,它也是用来度量图像分辨率的。每个像素颜色或灰度被量化后所占用的存储器位数越多,它能表达的颜色数目就越多,它的深度就越深。
·常见的图形/图像文件有以下几种。
·BMP(Bit Map Picture):PC上最常用的位图格式,有压缩和不压缩两种形式,该格式可表现从2位到24位的色彩,分辨率从480×320像素至1024×768像素。该格式在Windows环境下相当稳定,在文件大小没有限制的场合中运用极为广泛。
·DIF(Drawing Interchange Format):AutoCAD中的图形文件,它以ASCII方式存储图形,表现图形在尺寸大小方面十分精确,可以被CorelDraw、3DS等大型软件调用编辑。
·WMF(Windows Metafile Format):MicrosoftWindows图元文件,具有文件短小、图案造型化的特点。该类图形比较粗糙,并只能在MicrosoftOffice中调用编辑。
·GIF(Graphics Interchange Format):在各种平台的各种图形处理软件上均可处理的经过压缩的图形格式。缺点是存储色彩最高只能达到256种。
·JPG(Joint Photographic Expert Group):可以大幅度地压缩图形文件的一种图形格式。对于同一幅画面,JPG格式存储的文件是其他类型图形文件的1/10到1/20,而且色彩数最高可达到24位,所以它被广泛应用于Internet上的网页或Internet的图片库。
·TIF(Tagged Image File Format):文件体积庞大,但存储信息量亦巨大,细微层次的信息较多,有利于原稿阶调与色彩的复制。该格式有压缩和非压缩两种形式,最高支持的色彩数可达16M。
·PSD(Photoshop Standard):Photoshop中的标准文件格式,专门为Photoshop而优化的格式。
·8CDR(CorelDraw):CorelDraw的文件格式。另外,CDX是所有CorelDraw应用程序均能使用的图形(图像)文件,是发展成熟的CDR文件。
·SWF(Flash):Flash是Adobe公司制定的一种应用于Internet的动画格式,它是以矢量图作为基本的图像存储形式的。