第11章
可靠性及系统性能评价

模块化出题后，网络工程师考试涉及可靠性及系统性能评价的试题与软件设计师完全相同。而软件设计师考试中，历年此类型的题目，有很大的相似性。根据考试大纲，本章要求掌握的知识点如下：

·性能设计（系统调整、响应特性）；

·性能指标、性能评估（测试基准、系统监视器）；

·可靠性计算（MTBF、MTTR、可用性、故障率）；

·可靠性设计（失效安全、软失效、部件可靠性及系统可靠性的分配及估计）；

·可靠性指标和可靠性评估，RAS（可靠性、可用性和可维护性）。

下面我们通过具体的考试真题来学习和加强对本章知识点的掌握。

例题1（2005年5月试题7～8）

两个部件的可靠度R均为0.8，由这两个部件串联构成的系统的可靠度为　（7）　；由这两个部件并联构成的系统的可靠度为　（8）　。

（7）A．0.80

B．0.64

C．0.90

D．0.96

（8）A．0.80

B．0.64

C．0.90

D．0.96

例题分析

此题是一个串联系统可靠性计算的试题，它的计算方法是：

假设一个系统由n个子系统组成，当且仅当所有的子系统都能正常工作时，系统才能正常工作，这种系统称为串联系统，如图11-1所示。

图11-1　串联系统

设系统各个子系统的可靠性分别用R₁，R₂，…，R_n表示，则系统的可靠度R＝R₁×R₂×…×R_n。

如果系统的各个子系统的失效率分别用λ₁，λ₂，…，λ_n来表示，则系统的失效率λ＝λ₁＋λ₂＋…＋λ_n。

所以本题系统的可靠性R＝0.8×0.8＝0.64。

此外，并联系统的可靠性计算方法为：

假如一个系统由n个子系统组成，只要有一个子系统能够正常工作，系统就能正常工作，如图11-2所示。

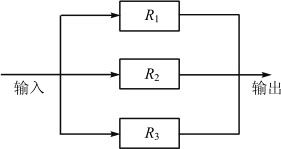
图11-2　并联系统

设系统各个子系统的可靠性分别用R₁，R₂，…，R_n表示，则系统的可靠性R＝1－（1－R₁）×（1－R₂）×…×（1－R_n）。所以本题系统可靠性R＝1－（1－0.8）²＝0.96

假如所有子系统的失效率均为λ，则系统的失效率为μ：

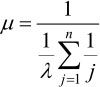
在并联系统中只有一个子系统是真正需要的，其余n－1个子系统称为冗余子系统，随着冗余子系统数量的增加，系统的平均无故障时间也增加了。

例题答案

（7）B

（8）D

例题2（2007年11月试题1）

若某计算机系统由两个部件串联构成，其中一个部件的失效率为7×10^-6/小时。若不考虑其他因素的影响，并要求计算机系统的平均故障间隔时间为10⁵小时，则另一个部件的失效率应为　（1）　／小时。

（1）A．2×10^-5

B．3×10^-5

C．4×10^-6

D．3×10^-6

例题分析

串联系统整体失效率为各系统失效率之和（不管各系统失效率是否一致），即

λ＝λ₁＋λ₂＋λ₃＋…＋λ_n

且平均无故障时间（MTBF）与失效率的关系为：MTBF＝1／λ，根据以上两个公式，可以列出如下：

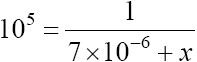，x为另一部件的失效率，解得x＝0.3×10^-5，即3×10^-6。

试题答案

（1）D

例题3（2007年5月试题4）

某系统的可靠性结构框图如图11-3所示。该系统由4个部件组成，其中2、3并联冗余，再与1、4部件串联构成。假设部件1、2、3的可靠度分别为0.90、0.70、0.70。若要求该系统的可靠度不低于0.75，则进行系统设计时，分配给部件4的可靠度至少应为　（4）　。

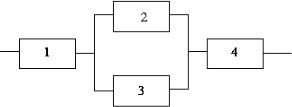
图11-3　系统图

（4）

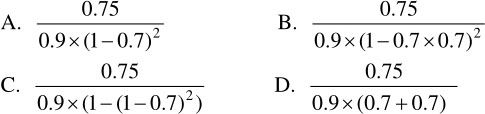
例题分析：

本题考查串、并联系统可靠度计算。

系统由部件2、3并联冗余，再与1、4部件串联构成。根据串联系统与并联系统可靠度的公式，R串联＝R₁×R₂×…×R_n，R并联＝1－（1－R₁）×（1－R₂）×…×（1－R_n）。不难得出答案为C。

例题答案

（4）C

例题4（2005年11月试题3）

某计算机系统的可靠性结构是如图11-4所示的双重串并联结构，若所构成系统的每个部件的可靠度为0.9，即R＝0.9，则系统的可靠度为　（3）　。

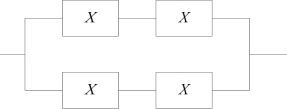
图11-4　先串联后并联系统

（3）A．0.9997

B．0.9276

C．0.9639

D．0.6561

例题分析

题目是一个先串联后并联的系统，计算时首先应该计算其中单个串联的两个部件组的可靠度，按公式计算得到其可靠度＝R×R；然后将串联的两个部件看成一个部件X，我们通过公式求两个部件X并联后的可靠度＝1－（1－R×R）²＝2R²－R⁴＝0.9639。

例题答案

（3）C

例题5（2006年11月试题2）

某计算机系统由图11-5所示的部件构成，假定每个部件X的千小时可靠度R均为0.9，则该系统的千小时可靠度约为　（2）　。

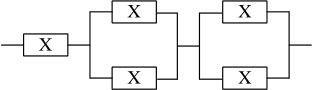
图11-5　先并联后串联系统

（2）A．0.882

B．0.951

C．0.9

D．0.99

例题分析

两个X并联的可靠度为：1－（1－0.9）²＝0.99。我们可以将两个并联的X部件看成一个部件X₁，X₂的可靠度为0.99，所以该系统的可靠度为：0.9×0.99×0.99＝0.88209。所以答案为A。

例题答案

（2）A

例题6（2011年5月试题4）

某计算机系统由图11-6所示的部件构成，假定每个部件的千小时可靠度都为R，则该系统的千小时可靠度为　（4）　。

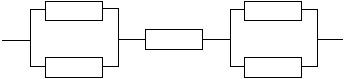
图11-6　部件构成图

（4）A．R＋2R/4

B．R＋R²/4

C．R（1－（1－R）²）

D．R（1－（1－R）²）²

例题分析

串联系统：假设一个系统由n个子系统组成，当且仅当所有的子系统都有能正常工作时，系统才能正常工作，这种系统称为串联系统。设系统各个子系统的可靠性分别用R₁，R₂，…，R_n表示，则系统的可靠性R＝R₁×R₂×…×R_n。

并联系统：假如一个系统由n个子系统组成，只要有一个子系统能够正常工作，系统就能正常工作。设系统各个子系统的可靠性分别用R₁，R₂，…，R_n表示，则系统的可靠性R＝1－（1－R₁）×（1－R₂）×…×（1－R_n）。

本题为串联系统与并联系统互连计算其可靠性，首先我们计算第一部分的可靠性，第一部分为并联系统，其可靠性为[1－（1－R）×（1－R）]，第二部分的可靠性为R，第三部分的可靠性为[1－（1－R）×（1－R）]。三个部分串联后的可靠性为R{[1－（1－R）×（1－R）]}²。

例题答案

（4）D